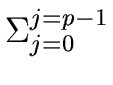

Next: Implementing Computer Algebra: basic ideas
Up: A review of complexity notions
Previous: Orders of magnitude
DIVIDE-AND-CONQUER ALGORITHMS proceed as follows.
- Divide
- the input problem into sub-problems.
- Conquer
- on the sub-problems by solving them directly if they are small
enough or proceed recursively.
- Combine
- the solutions of the sub-problems to obtain the solution of the
input problem.
EQUATION SATISFIED BY T(N).
Assume that the size of the input problem increases with an integer n.
Let T(n) be the time complexity of a divide-and-conquer algorithm
to solve this problem.
Then T(n) satisfies an equation of the form:
| T(n) = a T(n/b) + f (n). |
(13) |
where
f (n) is the cost of the combine-part, a 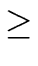 1 is the
number of recursively calls and n/b with b > 1
is the size of a sub-problem.
1 is the
number of recursively calls and n/b with b > 1
is the size of a sub-problem.
LABELED TREE ASSOCIATED WITH THE EQUATION.
Assume n is a power of b, say n = bp.
To solve this equation we can associate a labeled tree
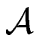 (n) to it
as follows.
(n) to it
as follows.
- (1)
- If n = 1, then
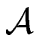 (n) is reduced to a single leaf by labeled T(1).
(n) is reduced to a single leaf by labeled T(1).
- (2)
- If n > 1, then the root of
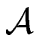 (n) is labeled
by f (n) and
(n) is labeled
by f (n) and
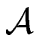 (n) possesses
a labeled sub-trees all equal to
(n) possesses
a labeled sub-trees all equal to
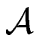 (n/b).
(n/b).
The labeled tree
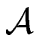 (n) associated with
T(n) = a T(n/b) + f (n)
has height p + 1.
Moreover the sum of its labels is T(n).
(n) associated with
T(n) = a T(n/b) + f (n)
has height p + 1.
Moreover the sum of its labels is T(n).
LET US GIVE TWO EXAMPLES.
- Consider the relation:
| T(n) = 2 T(n/2) + n2. |
(14) |
We obtain:
T(n) = n2 + 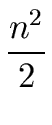 + + 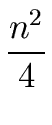 + + 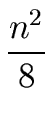 + ... + + ... + 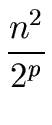 + n T(1). + n T(1). |
(15) |
Hence we have:
T(n) 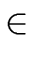  (n2). (n2). |
(16) |
- Consider the relation:
We obtain:
T(n) 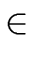  (log3(n)n). (log3(n)n). |
(18) |
A FORMULA TO ESTIMATE T(N).
Let a > 0 be an integer and let
S, T : 

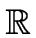 + be functions
such that
+ be functions
such that
- (i)
-
S(2 n)
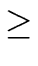 2 S(n) and
S(n)
2 S(n) and
S(n) 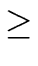 n.
n.
- (ii)
- If n = 2p then
T(n)
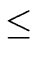 a T(n/2) + S(n).
a T(n/2) + S(n).
Then for n = 2p we have
- (1)
- if a = 1 then
T(n) 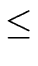 (2 - 2/n) S(n) + T(1) (2 - 2/n) S(n) + T(1) 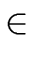 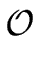 (S(n)), (S(n)), |
(19) |
- (2)
- if a = 2 then
T(n) 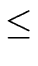 S(n) log2(n) + T(1) n S(n) log2(n) + T(1) n 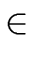 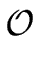 (log2(n) S(n)), (log2(n) S(n)), |
(20) |
- (3)
- if a
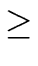 3 then
3 then
T(n) 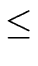 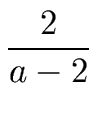  nlog2(a)-1 - 1 nlog2(a)-1 - 1 S(n) + T(1) nlog2(a) S(n) + T(1) nlog2(a)   (S(n) nlog2(a)-1). (S(n) nlog2(a)-1). |
(21) |
Indeed
| T(2p) |
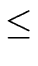 |
a T(2p-1) + S(2p) |
| |
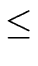 |
a a T(2p-2) + S(2p-1) a T(2p-2) + S(2p-1)![$\displaystyle \left.\vphantom{ a \, T(2^{p-2}) + S(2^{p-1}) }\right]$](img31.png) + S(2p) + S(2p) |
| |
= |
a2 T(2p-2) + a S(2p-1) + S(2p) |
| |
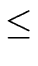 |
a2 a T(2p-3) + S(2p-2) a T(2p-3) + S(2p-2)![$\displaystyle \left.\vphantom{ a \, T(2^{p-3}) + S(2^{p-2}) }\right]$](img33.png) + a S(2p-1) + S(2p) + a S(2p-1) + S(2p) |
| |
= |
a3 T(2p-3) + a2 S(2p-2) + a S(2p-1) + S(2p) |
| |
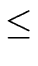 |
ap T(1) + 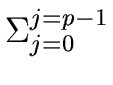 aj S(2p-j) aj S(2p-j) |
|
(22) |
Moreover
| S(2p) |
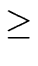 |
2 S(2p-1) |
| S(2p) |
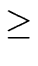 |
22 S(2p-2) |
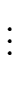 |
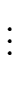 |
 |
| S(2p) |
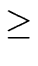 |
2j S(2p-j) |
|
(23) |
Thus
Hence
T(2p) 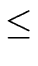 ap T(1) + S(2p) ap T(1) + S(2p) 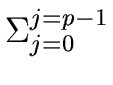 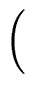 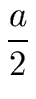 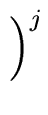 . . |
(25) |
For a = 1 we obtain
| T(2p) |
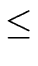 |
T(1) + S(2p) 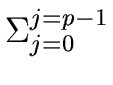  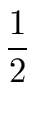  |
| |
= |
T(1) + S(2p) 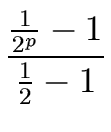 |
| |
= |
T(1) + S(n) (2 - 2/n). |
|
(26) |
For a = 2 we obtain
| T(2p) |
 |
2p T(1) + S(2p) p |
| |
= |
n T(1) + S(n) log2(n). |
|
(27) |


Next: Implementing Computer Algebra: basic ideas
Up: A review of complexity notions
Previous: Orders of magnitude
Marc Moreno Maza
2004-04-27
![]() (n) to it
as follows.
(n) to it
as follows.
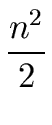 +
+ 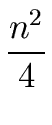 +
+ 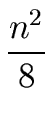 + ... +
+ ... + 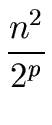 + n T(1).
+ n T(1).![]()
![]()
![]() + be functions
such that
+ be functions
such that
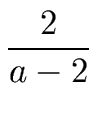
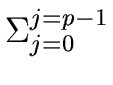 aj S(2p-j)
aj S(2p-j)