

Next: Rational numbers.
Up: How to encode the elements
Previous: How to encode the elements
One machine word can contain a SINGLE PRECISION
INTEGER in the range
[0, 2N - 1].
To represent integers outside of this range, so called
MULTIPRECISION INTEGER, we use arrays of N-bit words.
To be precise we consider the 2N-ary (or radix 2N)
expansion of a nonzero integer:
a = (- 1)s 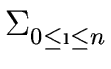 ai2Ni ai2Ni |
(32) |
where
- every
ai
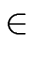 [0, 2N - 1] is a digit in
the 2N-ary expansion of a,
[0, 2N - 1] is a digit in
the 2N-ary expansion of a,
-
s
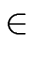 {0, 1} determines the sign of a,
{0, 1} determines the sign of a,
-
n + 1
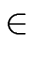 [1, 2N] is the number of 2N-digits in
the 2N-ary expansion of a,
[1, 2N] is the number of 2N-digits in
the 2N-ary expansion of a,
-
an
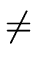 0.
0.
Then the integer a with (n + 1) 2N-digits
can be represented by an array (of N-bit words)
with length n + 3 since we need
- one word for s and
- one word for n
The reasonable UNIT OPERATION for integers
is the the WORD OPERATION.
One can easily check that
- the ADDITION of two integers with
at most n 2N-digits requires
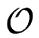 (n) word operations
(n) word operations
- the MULTIPLICATION of two integers with
at most n 2N-digits requires
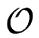 (n2) word operations.
(n2) word operations.


Next: Rational numbers.
Up: How to encode the elements
Previous: How to encode the elements
Marc Moreno Maza
2004-04-27
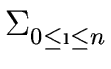 ai2Ni
ai2Ni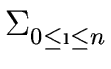 ai2Ni
ai2Ni