

Next: Multivariate polynomials.
Up: How to encode the elements
Previous: Real algebraic numbers.
Let R be a ring. The univariate polynomial ring R[x]
can be implemented using different data types.
- Expression trees.
- All arithmetic operations are in
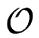 (1).
But the representation is not canonical:
two different expression trees can encode the same polynomial.
Therefore operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM
are in
(1).
But the representation is not canonical:
two different expression trees can encode the same polynomial.
Therefore operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM
are in
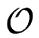 (n) where n is the degree of the polynomial.
Even worst the equality-test is
(n) where n is the degree of the polynomial.
Even worst the equality-test is
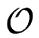 (n2) (for non-balanced trees).
(n2) (for non-balanced trees).
- Arrays of coefficients.
- The polynomial
| p(x) = anxn + ... + a1x + a0 |
(33) |
is coded by a record consisting of
- a single integer s,
- a single integer
d
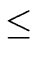 s + 1,
s + 1,
- an array of size s such that
a0 + ... + anxn is represented by
[a0,..., an,...]
and d = n.
This representation is said dense
becasue all ai are coded, even those which are null.
This representation is canonical.
Hence operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM are in
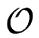 (1).
Addition and equality-test are in
(1).
Addition and equality-test are in
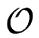 (n) and multiplication
is in
(n) and multiplication
is in
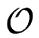 (n2).
This representation is especially good when the ring of coefficients
is a small prime field, i.e.
(n2).
This representation is especially good when the ring of coefficients
is a small prime field, i.e.
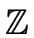 /p
/p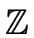 with p prime and
in the range
[2, 2N - 1].
with p prime and
in the range
[2, 2N - 1].
- List of terms.
- The polynomial
| p(x) = anxn + ... + a1x + a0 |
(34) |
is coded by the list L of records [ai, i]
where ai is a nonzero coefficient
and such that L is sorted decreasingly w.r.t. i.
This representation is said sparse,
since only the nonzero ai are coded.
This representation is also canonical.
Hence operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM are in
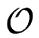 (1).
Moreover the operation REDUCTUM does not require
coefficient duplication (on the contrary of the previous
representation).
Addition and equality-test are in
(1).
Moreover the operation REDUCTUM does not require
coefficient duplication (on the contrary of the previous
representation).
Addition and equality-test are in
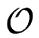 (n) and multiplication
is in
(n) and multiplication
is in
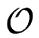 (n2).
This representation is especially good when the ring of coefficients
is itself a ring of sparse polynomials.
(n2).
This representation is especially good when the ring of coefficients
is itself a ring of sparse polynomials.


Next: Multivariate polynomials.
Up: How to encode the elements
Previous: Real algebraic numbers.
Marc Moreno Maza
2004-04-27
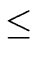 s + 1,
s + 1,