Theorem 2
Let
n be a power of 2 and
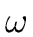
 R
R a primitive
n-th
root of unity.
Then convolution in
R[
x]/
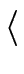 xn
xn-1
and
multiplication in
R[
x] of polynomials whose product has degree less than
n
can be performed using
-
3 n log(n) additions in R,
-
3/2 n log(n) + n - 2 multiplications by a power of
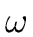 ,
,
- n multiplications in R,
- n divisions by n (as an element of R),
leading to
9/2
n log(
n) +

(
n) operations in
R.
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $f,g \in ...
...\gamma}) \ = \ 1/n \, DTF_{{\omega}^{-1}}({\gamma})$\end{tabbing}\end{minipage}}](img90.png)