Next: Questions Up: Exercise 5 Previous: Exercise 5
![$ m \in {\mbox{${\mathbb{K}}$}}[x]$](img82.png) be a polynomial of degree
be a polynomial of degree 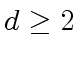 .
We aim at computing in
.
We aim at computing in
![$ {\mbox{${\mathbb{K}}$}}[x] / \langle m \rangle$](img84.png) as fast
as possible.
Let
as fast
as possible.
Let
![$ {\ell} \in {\mbox{${\mathbb{K}}$}}[x]$](img85.png) be another polynomial with degree
strictly less than
be another polynomial with degree
strictly less than ![$ u, v \in {\mbox{${\mathbb{K}}$}}[x]$](img87.png) such that
such that
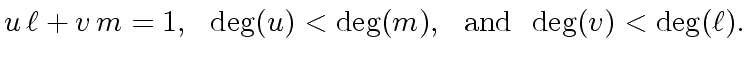 |
![$ {\mbox{${\mathbb{K}}$}}[x] / \langle m \rangle$](img84.png) to itself
mapping
to itself
mapping
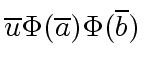 can be computed in
can be computed in
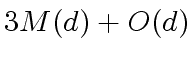 operations in
operations in
![$ \overline{a}, \overline{b} \in {\mbox{${\mathbb{K}}$}}[x] / \langle m \rangle$](img94.png) define
define
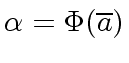 and
and
 .
Then,
.
Then,
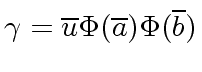 .
.
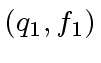 be the quotient-and-remainder
in the division of
be the quotient-and-remainder
in the division of
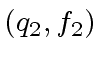 be the quotient-and-remainder
in the division of
be the quotient-and-remainder
in the division of 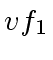 by
by 
Marc Moreno Maza