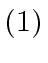
- Design a modular modular algorithm based on the following observation:
if
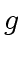 divides
divides 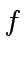 then
then 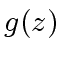 divides
divides 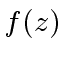 for every
for every
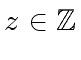 .
.
- Assume that we are given an upper bound for the absolute value
of a coefficient in any polynomial
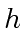 dividing
dividing 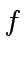 .
(Such upper bound exists and will be discussed in class.)
Design a modular modular algorithm based on the following observation:
if
.
(Such upper bound exists and will be discussed in class.)
Design a modular modular algorithm based on the following observation:
if 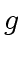 divides
divides 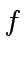 (in
(in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) ) then
) then 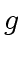 divides
divides 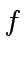 modulo any prime number
modulo any prime number 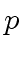 .
.

- No complexity analysis is required.
However, you are asked to suggest why the second algorithm
is likely to be more efficient that the first one.
Marc Moreno Maza
2008-03-18
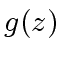 divides
divides 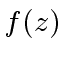 for every
for every
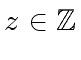 .
.
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) ) then
) then