Let 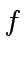 and
and 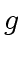 in
in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) be two polynomials with respective degrees
be two polynomials with respective degrees
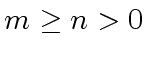 .
We assume that
.
We assume that 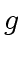 is monic, that is, its leading coefficient is
is monic, that is, its leading coefficient is 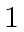 .
Let
.
Let  and
and 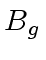 be upper bounds for the absolute value of a coefficient
in
be upper bounds for the absolute value of a coefficient
in 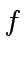 and
and 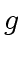 respectively.
We aim at computing the quotient
respectively.
We aim at computing the quotient 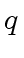 and the remainder
and the remainder 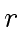 in the division of
in the division of 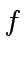 by
by 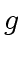 by means of a modular method.
by means of a modular method.
Marc Moreno Maza
2008-03-18
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) be two polynomials with respective degrees
be two polynomials with respective degrees
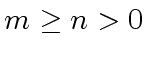 .
We assume that
.
We assume that