Next: Questions Up: Exercise 2 Previous: Exercise 2
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) be two polynomials of degree at most
be two polynomials of degree at most 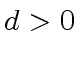 .
Let
.
Let  is an upper bound for the absolute value of a coefficient
in the product
is an upper bound for the absolute value of a coefficient
in the product 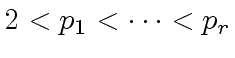 such that their product
such that their product 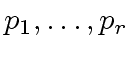 fits in a machine word,
fits in a machine word,
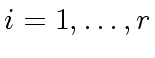 , can be done
, can be done
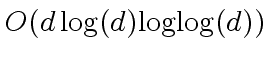 machine word operations.
machine word operations.