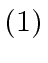
- Define
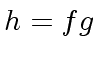 in
in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) . Assume that
. Assume that 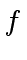 and
and 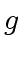 have degree
have degree 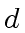 and define:
and define:
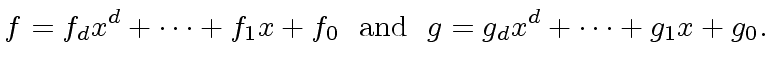 |
(18) |
Then define:
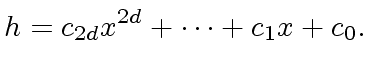 |
(19) |
For all
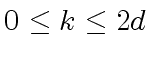 , we have:
, we have:
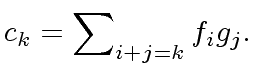 |
(20) |
Observe that, for a given 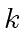 in the range
in the range
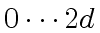 ,
the number of products
,
the number of products 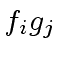 is at most
is at most 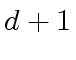 .
Indeed, the polynomials
.
Indeed, the polynomials 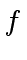 and
and 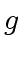 have
have 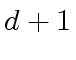 terms.
From there, we deduce that for all
terms.
From there, we deduce that for all
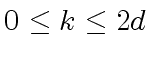 , we have:
, we have:
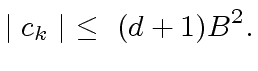 |
(21) |
- One can proceed as follows:
- Let
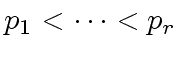 machine-word-size
odd primes such that their product
machine-word-size
odd primes such that their product 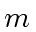 exceeds
exceeds 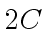
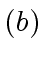
- For all
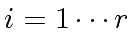 compute
compute
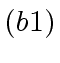
- the images
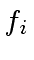 and
and 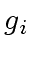 of
of 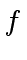 and
and 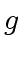 in
in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) ,
,
- the product
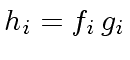 in
in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) .
.

- Using the Chinese Remaindering Algorithm coefficient-wise,
reconstruct
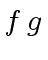 from
from
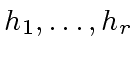 .
.
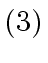
- We give complexity estimates (upper bounds for the number of machine-word
operations) for each of the steps
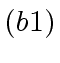 ,
, 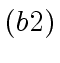 and
and  above.
For the operations on integers, we use bounds based on classical
quadratic algorithms (not fast ones, since they were not discussed
in class).
Let
above.
For the operations on integers, we use bounds based on classical
quadratic algorithms (not fast ones, since they were not discussed
in class).
Let 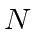 be the length of a machine-word, let
be the length of a machine-word, let
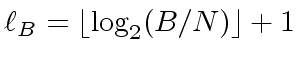 be the number of machine-words to write
be the number of machine-words to write 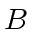 and let
and let
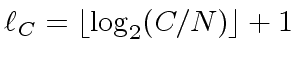 to write
to write 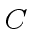 .
.
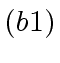
-
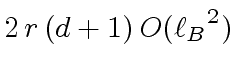 machine-word operations
machine-word operations
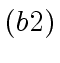
-
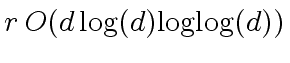 machine-word operations
machine-word operations

-
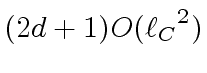 machine-word operations
machine-word operations
Marc Moreno Maza
2008-03-18
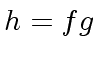 in
in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) . Assume that
. Assume that 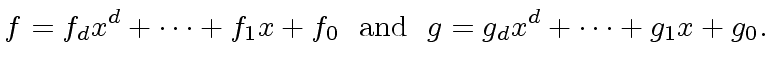
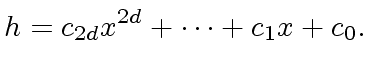
 , we have:
, we have:
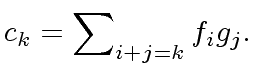
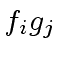 is at most
is at most 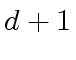 .
Indeed, the polynomials
.
Indeed, the polynomials 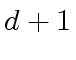 terms.
From there, we deduce that for all
terms.
From there, we deduce that for all
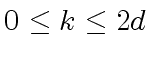 , we have:
, we have:
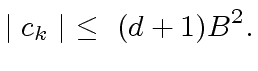
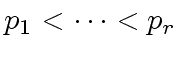 machine-word-size
odd primes such that their product
machine-word-size
odd primes such that their product 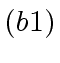
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) ,
,
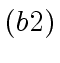
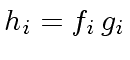 in
in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) .
.
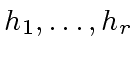 .
.
 ,
,  and
and 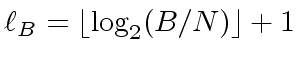 be the number of machine-words to write
be the number of machine-words to write 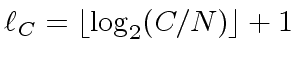 to write
to write 
 machine-word operations
machine-word operations
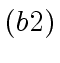
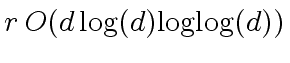 machine-word operations
machine-word operations
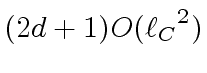 machine-word operations
machine-word operations