Next: Questions Up: Exercise 1 Previous: Exercise 1
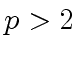 be a prime integer.
Let
be a prime integer.
Let ![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img4.png) be two polynomials with respective degrees
be two polynomials with respective degrees
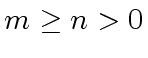 .
We aim at computing the product
.
We aim at computing the product  does not divide
does not divide  .
Hence, there are no
.
Hence, there are no 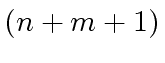 -th primitive roots of unity in
-th primitive roots of unity in
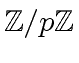 and the FFT-based algorithm studied in class does not apply in this context.
However, we assume that we can find
and the FFT-based algorithm studied in class does not apply in this context.
However, we assume that we can find 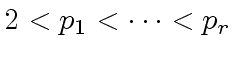 such that:
such that:
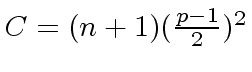 ,
,
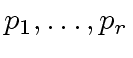 fits in a machine word,
fits in a machine word,
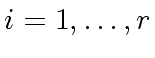 , the integer
, the integer  divides
divides 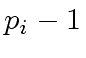 ,
such that, regarding
,
such that, regarding ![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img18.png) , one can compute the product
, one can compute the product ![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img18.png) using the FFT-based algorithm studied in class.
using the FFT-based algorithm studied in class.
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img4.png) .
.
Marc Moreno Maza