Next: Questions Up: Exercise 2 Previous: Exercise 2
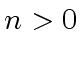 be a power of
be a power of  and
and
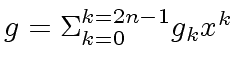 be two polynomials in
be two polynomials in
![$ {\mbox{${\mathbb{R}}$}}[x]$](img31.png) with degrees less than
with degrees less than 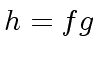 has degree less than
has degree less than 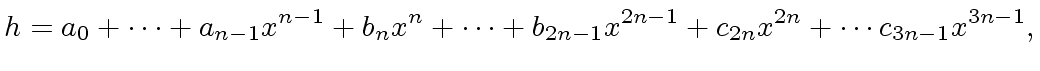 |
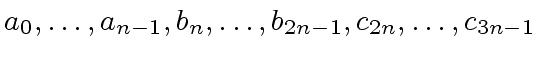 belong to
belong to
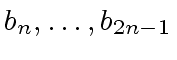 at the cost of multiplying
two polynomials in
at the cost of multiplying
two polynomials in
![$ {\mbox{${\mathbb{R}}$}}[x]$](img31.png) with degree
with degree 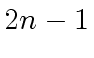 .
The polynomial
.
The polynomial
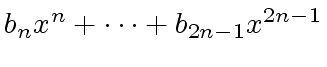 is called the middle product of
is called the middle product of Marc Moreno Maza