Next: Modular computation of the determinant Up: Modular Computation Previous: Modular Computation
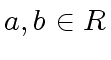 the relation
the relation
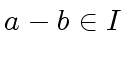 |
(96) |
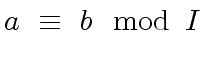 |
(97) |
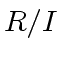 where addition and multiplication are defined by
where addition and multiplication are defined by
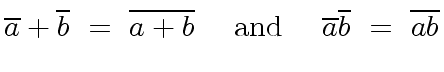 |
(98) |
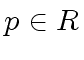 with
with  .
We consider the ideal
.
We consider the ideal 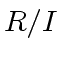 is often denoted by
is often denoted by 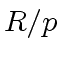 and the class of
and the class of 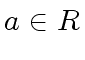 in
in 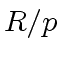 by
by
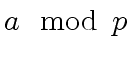 .
For
.
For
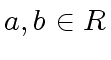 the relation
the relation
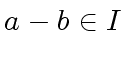 means
that
means
that 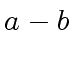 is a multiple of
is a multiple of 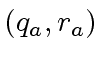 and
and 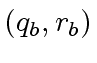 be the quotient-remainder
pairs of
be the quotient-remainder
pairs of 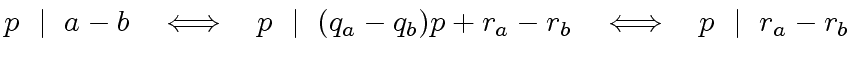 |
(99) |
![$ R = {\bf k}[x]$](img19.png) we have in fact
we have in fact
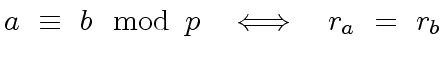 |
(100) |
![$ R = {\bf k}[x]$](img19.png) for a field
for a field  and let
and let  .
For every
.
For every  there exists
there exists 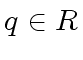 such that
such that
 |
(101) |
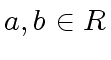 we have
we have
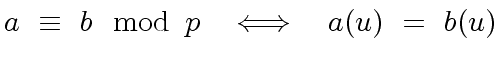 |
(102) |
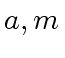 be in
be in 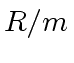 iff
iff
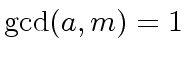 .
In this case the Extended Euclidean Algorithm can be used
to compute the inverse of
.
In this case the Extended Euclidean Algorithm can be used
to compute the inverse of
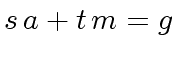 |
(103) |
 then
then
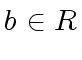 such that
such that
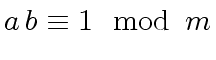 |
(104) |
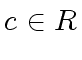 such that
such that
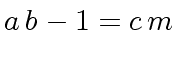 .
If
.
If 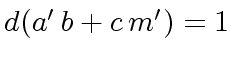 ).
Hence
).
Hence
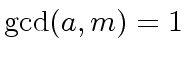 .
.
ResidueClassRing(R:EuclideanDomain, p:R): Ring with {
class: R -> %;
sample: % -> R;
} == R add {
Rep == R;
import from R;
1: % == per(1);
0: % == per(0);
zero?(x:%): Boolean == zero?(rep(x));
(x:%) = (y:%) : Boolean == zero?(x-y);
one?(x:%): Boolean == x = 1;
class(a:R):% == {
(q,r) := divide(a,p);
per(r);
}
sample(x:%): R == rep(x);
(x:%) + (y:%) : % == class(rep(x) + rep(y));
-(x:%) : % == class(-rep(x));
(x:%) * (y:%) : % == class(rep(x) * rep(y));
(n:Integer) * (x:%): % == class(n * rep(x));
(x:%) ^ (n:NonNegativeInteger) : % == class(rep(x) ^ n);
recip(x:%): Partial(%) == {
import from Partial(%);
(u,v,g) := extendedEuclidean(rep(x),p);
h?: Partial(R) := recip(g);
failed? h? => failed();
h: R := retract(h?);
[class(h * u)];
}
}
![$ f \in {\bf k}[x]$](img202.png) with degree
with degree
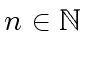 .
One arithmetic operation in the residue class ring
.
One arithmetic operation in the residue class ring
![$ {\bf k}[x]/f$](img460.png) ,
that is, addition, multiplication or division by
an invertible element can be done using
,
that is, addition, multiplication or division by
an invertible element can be done using
 arithmetic operations in
arithmetic operations in
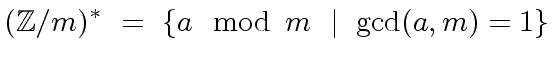 |
(105) |
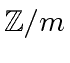 .
The Euler's totient function
.
The Euler's totient function
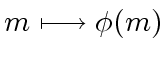 counts the number of elements of
counts the number of elements of
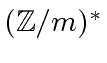 .
By convention
.
By convention
 .
Then if
.
Then if 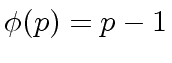 .
If
.
If 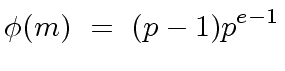 |
(106) |
 is a prime and
is a prime and
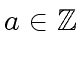 then we have
then we have
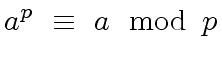 |
(107) |
 .
. which we do by induction on
which we do by induction on 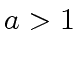 we have
we have
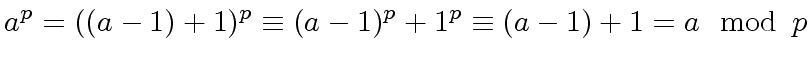 |
(108) |
 and
and
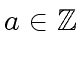 such that
such that
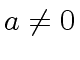 and such that
and such that 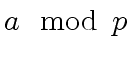 can be computed by
can be computed by
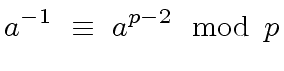 |
(109) |
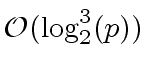 word operations.
Is this better than the modular inversion
via Euclide's algorithm?
word operations.
Is this better than the modular inversion
via Euclide's algorithm?
Marc Moreno Maza