Next: The Chinese Remaindering Algorithm Up: Interpolation and Rational Reconstruction Previous: Interpolation and Rational Reconstruction
Let ![]() be a field and let
be a field and let
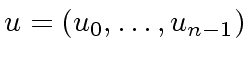 be a sequence of pairwise distinct elements of
be a sequence of pairwise distinct elements of ![]() .
.
![$ {\bf k}[x]$](img191.png) with degree
with degree 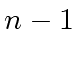 , say
, say
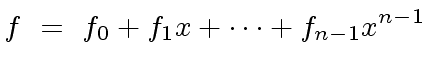 |
(35) |
 using Horner's rule
using Horner's rule
 |
(36) |
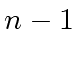 additions and
additions and 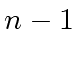 multiplications leading to
multiplications leading to
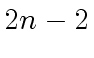 operations in the base field
operations in the base field 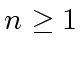 .
.
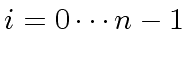 the
the 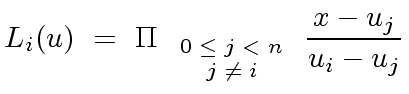 |
(37) |
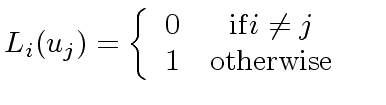 |
(38) |
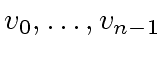 be in
be in ![$ f \in {\bf k}[x]$](img202.png) with degree less than
with degree less than
![$ f \in {\bf k}[x]$](img202.png) of degree less than
of degree less than 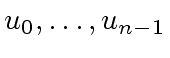 or computing an interpolating polynomial at these points
can be done in
or computing an interpolating polynomial at these points
can be done in
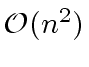 operations in
operations in 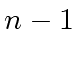 at one point costs
at one point costs 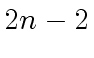 operations in
operations in 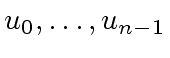 amounts to
amounts to
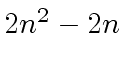 .
Let us prove now that interpolating a polynomial at
.
Let us prove now that interpolating a polynomial at
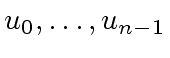 can be done in
can be done in
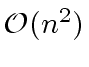 operations in
operations in 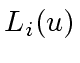 .
Consider
.
Consider 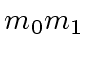 ,
,
 , ...
, ...
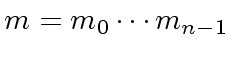 where
where 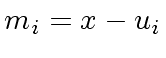 .
Let
.
Let
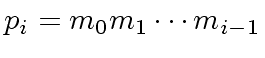 and
and
 for
for
 |
(41) |
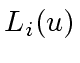 's let us start with that of
's let us start with that of 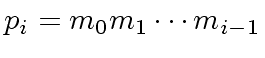 of degree
of degree 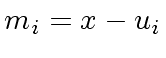 of degree
of degree 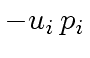 plus
plus
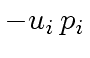 (of degree
(of degree 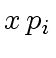 (of degree
(of degree 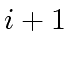 but without constant term)
but without constant term)
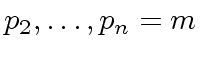 amounts to
amounts to
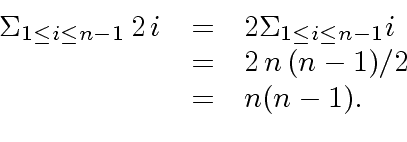 |
(42) |
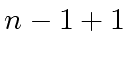 steps, each step requiring
steps, each step requiring 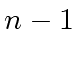 computing each
computing each  's
amounts to
's
amounts to 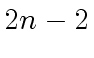 operations in the base field
operations in the base field  's amounts to
's amounts to
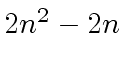 .
Then computing each
.
Then computing each
 from the
from the  's costs
's costs 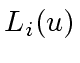 's from scratch
amounts to
's from scratch
amounts to
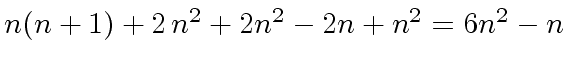 .
.
Computing ![]() from the
from the 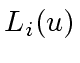 's requires
's requires
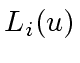 (which is a polynomial of degree
(which is a polynomial of degree 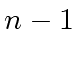 ) by the number
) by the number 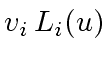 leading to
leading to 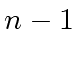 additions
of polynomials of degree at most
additions
of polynomials of degree at most 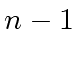 costing
costing 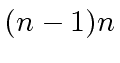 operations in
operations in 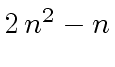 .
Finally the total cost is
.
Finally the total cost is
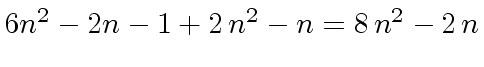 .
.
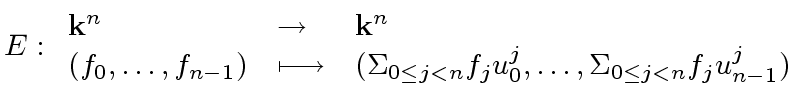 |
(43) |
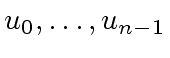 .
It is obvious that
.
It is obvious that 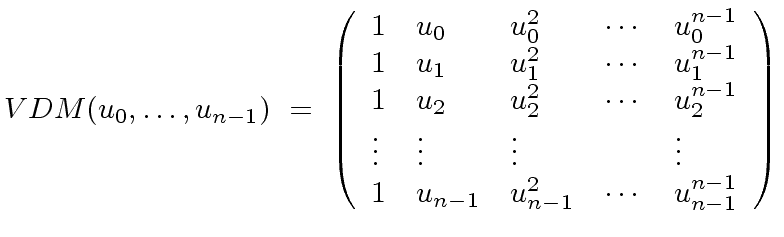 |
(44) |
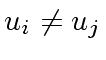 for all
for all
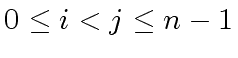 .
To conclude observe that both
evaluation and interpolation
are linear maps between coefficients and value vectors.
.
To conclude observe that both
evaluation and interpolation
are linear maps between coefficients and value vectors.
Marc Moreno Maza