Next: Modular Computation Up: Interpolation and Rational Reconstruction Previous: The Chinese Remaindering Algorithm
Let ![]() be a field, let
be a field, let
![$ m \in {\bf k}[x]$](img369.png) be a polynomial
of degree
be a polynomial
of degree  .
Given a polynomial
.
Given a polynomial
![$ f \in {\bf k}[x]$](img202.png) of degree less than
of degree less than ![]() and an integer
and an integer
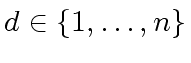 , we want to find a rational
function
, we want to find a rational
function
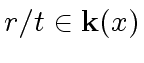 with
with
![$ r,t \in {\bf k}[x]$](img373.png) satisfying
satisfying
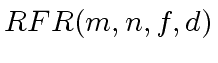 .
A solution to this problem is also a solution to the following
weaker problem: compute a rational
function
.
A solution to this problem is also a solution to the following
weaker problem: compute a rational
function
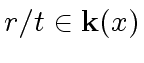 with
with
![$ r,t \in {\bf k}[x]$](img373.png) satisfying
satisfying
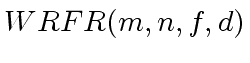 .
.
We recall that a rational function
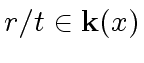 is said to be in canonical form if
is said to be in canonical form if ![]() is monic
and if
is monic
and if
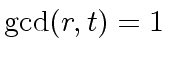 .
Clearly, every rational function has a unique canonical form.
.
Clearly, every rational function has a unique canonical form.
The following Theorem 5:
 has always a solution,
which can be computed by an algorithm,
has always a solution,
which can be computed by an algorithm,
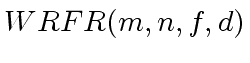 to be a solution of
to be a solution of
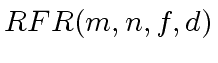 ,
,
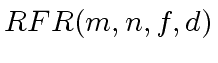 to have a solution.
to have a solution.
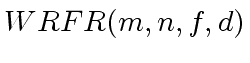 and
and
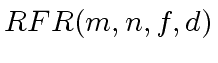 .
.
![$ r_j, s_j, t_j \in {\bf k}[x]$](img379.png) be the
be the 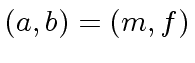 where
where 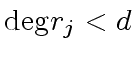 .
.
 is a solution to
problem
is a solution to
problem
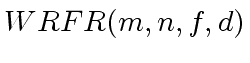 .
.
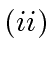
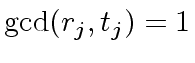 , then the couple
, then the couple
 is a solution to
problem
is a solution to
problem
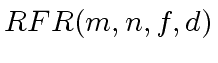 .
.
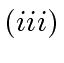
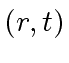 is a solution to problem
is a solution to problem
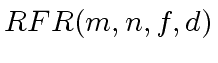 and if
and if 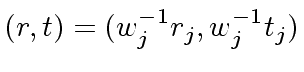 where
where
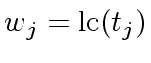 .
.
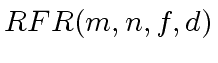 admits a solution if and only if
admits a solution if and only if
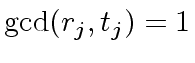 .
.
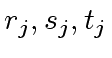 are uniquely defined.
Indeed, we have
are uniquely defined.
Indeed, we have
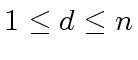 and,
and,
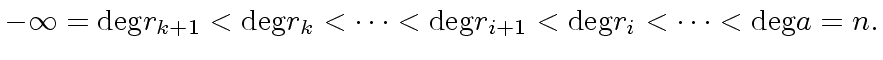 |
(88) |
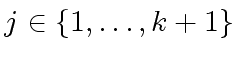 such that
we have
such that
we have
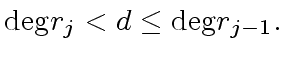 |
(89) |
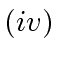 of Proposition 1 we have
of Proposition 1 we have
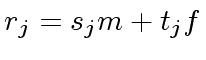 |
(90) |
 .
From Proposition 2, we deduce
.
From Proposition 2, we deduce
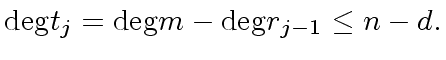 |
(91) |
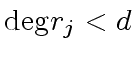 holds, we have proved that
holds, we have proved that
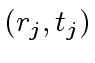 is a solution to
problem
is a solution to
problem
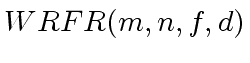 .
This shows
.
This shows  .
We assume that
.
We assume that
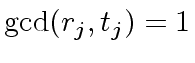 holds.
From Point
holds.
From Point  of Proposition 1
we have
of Proposition 1
we have
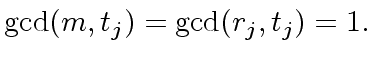 |
(92) |
 .
Hence, under the assumption
.
Hence, under the assumption
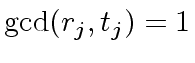 ,
the couple
,
the couple
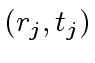 is also a solution to
is also a solution to
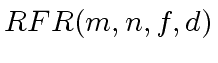 .
.
Next, we prove 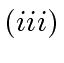 .
So we consider
.
So we consider 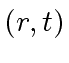 a solution to
a solution to
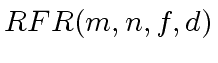 such that the fraction
such that the fraction ![]() is in canonical form.
There exists
is in canonical form.
There exists
![$ s \in {\bf k}[x]$](img398.png) such that we have
such that we have
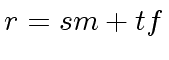 .
Since
.
Since
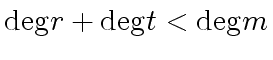 holds,
we can apply Proposition 3.
So, let
holds,
we can apply Proposition 3.
So, let
 be such that
be such that
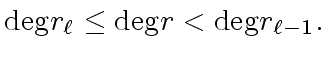 |
(93) |
![$ {\alpha} \in {\bf k}[x]$](img158.png) such that
such that
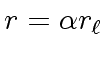 and
and
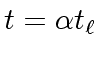 both hold.
both hold.
If
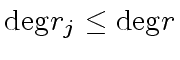 then we have
then we have
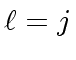 .
If
.
If
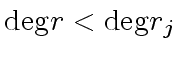 then we have
then we have
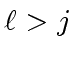 .
.
We prove that
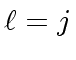 holds.
If
holds.
If 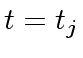 then
then
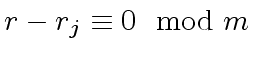 ,
and thus
,
and thus 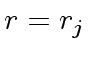 , since
, since
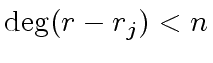 holds,
which implies
holds,
which implies
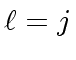 .
If
.
If
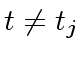 , we can apply Proposition 3
again.
Then, there exists
, we can apply Proposition 3
again.
Then, there exists
![$ {\beta} \in {\bf k}[x]$](img414.png) such that
such that
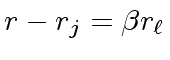 and
and
 both hold.
It follows that we have
both hold.
It follows that we have
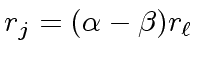 and
and
 .
Hence, we deduce
.
Hence, we deduce
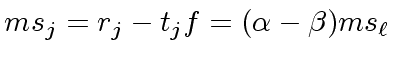 |
(94) |
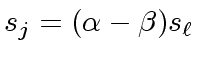 .
Since
.
Since
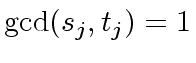 holds
we must have
holds
we must have
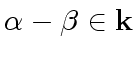 and thus
and thus
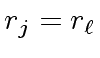 .
Therefore, we have proved that
.
Therefore, we have proved that
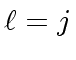 holds.
This implies
holds.
This implies
 |
(95) |
 and
and
 hold.
This proves
hold.
This proves 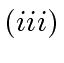 .
Finally,
.
Finally, 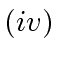 follows from
follows from 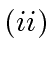 and
and 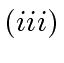 .
.
Marc Moreno Maza