Proof.
We apply Theorem
![[*]](crossref.png)
with
 |
(10) |
Thus we have
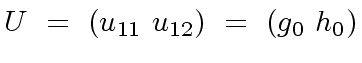 |
(11) |
Observe that this matrix is left-invertible modulo

if and only if
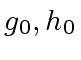
are relatively prime modulo

.
Indeed, the matrix

is left-invertible modulo

iff there exists
a matrix
such that
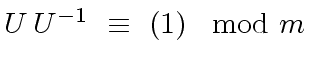
, that is
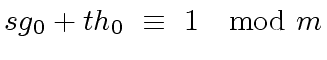 |
(12) |
We prove now the claim of the theorem.
Assume we have computed
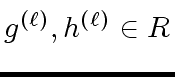
such that

and
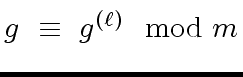
hold.
We want to compute
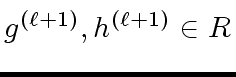
.
Let

be such that
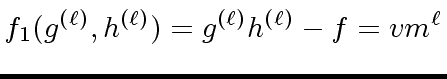 |
(13) |
We look for
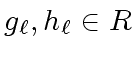
such that
 |
(14) |
Following the proof of Theorem
![[*]](crossref.png)
we are led to solve the equation
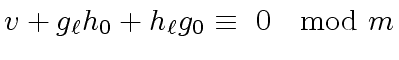 |
(15) |
A solution of this equation is
 |
(16) |
This proves the claim of the theorem.

Proof.
By induction on
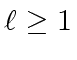
.
The clain is clear for
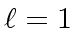
.
So let us assume it is true for
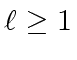
and consider monic polynomials
![$ g^{({\ell}+1)}, h^{({\ell}+1)} \in R[x]$](img83.png)
satisfying
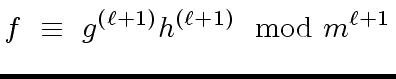 |
(18) |
and
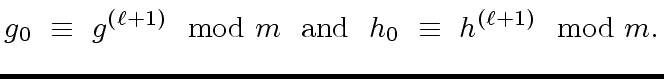 |
(19) |
Such polynomials
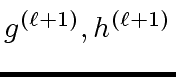
exist
by Theorem
3.
(The fact that they can be chosen monic is left to the reader
as an exercise.)
Observe that we have
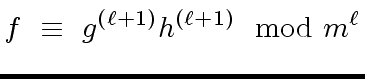 |
(20) |
So the induction hypothesis leads to
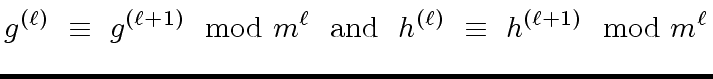 |
(21) |
Hence there exist polynomials
![$ q_g, q_h \in (R/m)[x]$](img89.png)
such that
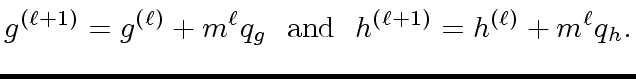 |
(22) |
Since
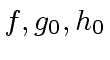
are given to be monic, it is easy to prove
that for

we have
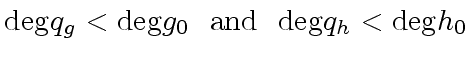 |
(23) |
In addition, observe that combining
Equation (
18)
and
Equation (
22)
we obtain
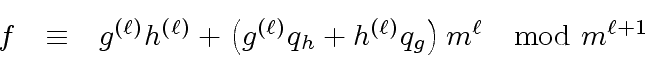 |
(24) |
The induction hypothesis shows that

is a multiple of
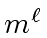
.
Then we obtain
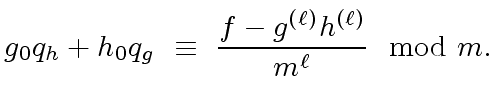 |
(25) |
By Theorem
1
and
Equation (
23),
the Equation (
25)
has a unique solution.

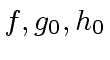 be univariate polynomials in
be univariate polynomials in ![$ R[x]$](img50.png) and let
and let 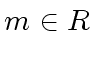 .
We assume that the following relation holds
.
We assume that the following relation holds
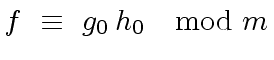
 such that
such that
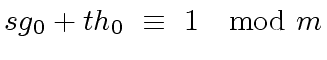
![$ g^{({\ell})}, h^{({\ell})} \in R[x]$](img59.png) such that we have
such that we have
 ,
,
 .
.
![[*]](crossref.png) with
with

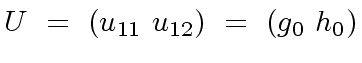
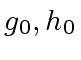 are relatively prime modulo
are relatively prime modulo 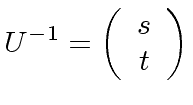
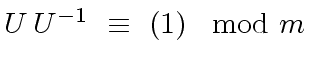 , that is
, that is
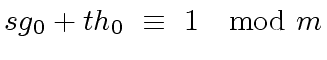
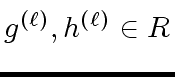 such that
such that
 and
and
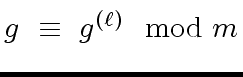 hold.
We want to compute
hold.
We want to compute
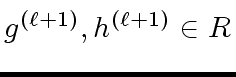 .
Let
.
Let 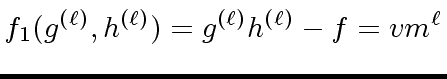
 such that
such that

![[*]](crossref.png) we are led to solve the equation
we are led to solve the equation

 to
Equation (15).
It is desirable to add constraints such that
Equation (15)
has a unique soulution.
In particular, one would like to guarantee that for every integer
to
Equation (15).
It is desirable to add constraints such that
Equation (15)
has a unique soulution.
In particular, one would like to guarantee that for every integer  and
and  be univariate monic polynomials in
be univariate monic polynomials in ![$ R[x]$](img50.png) .
Let
.
Let 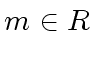 be such that
be such that 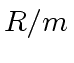 is a field.
We assume that the following relation holds
is a field.
We assume that the following relation holds
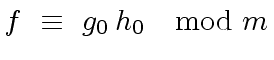
![$ g^{({\ell})}, h^{({\ell})} \in R[x]$](img59.png) such that we have
such that we have
 ,
,
 ,
,
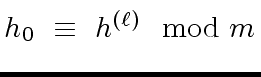 .
.
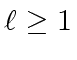 .
The clain is clear for
.
The clain is clear for
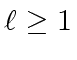 and consider monic polynomials
and consider monic polynomials
![$ g^{({\ell}+1)}, h^{({\ell}+1)} \in R[x]$](img83.png) satisfying
satisfying
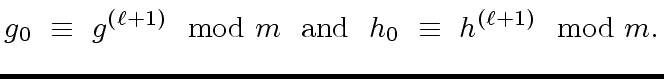
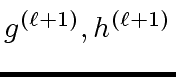 exist
by Theorem 3.
(The fact that they can be chosen monic is left to the reader
as an exercise.)
Observe that we have
exist
by Theorem 3.
(The fact that they can be chosen monic is left to the reader
as an exercise.)
Observe that we have
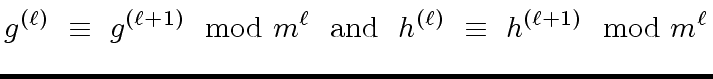
![$ q_g, q_h \in (R/m)[x]$](img89.png) such that
such that
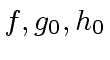 are given to be monic, it is easy to prove
that for
are given to be monic, it is easy to prove
that for  we have
we have
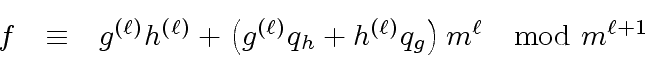
 is a multiple of
is a multiple of