- OBSERVATIONS.
- Computer algebra algorithms perform symbolic computations:
numbers are manipulated by using their mathematical definitions.
- Hence results are exact and complete.
- However they can be huge!
- Moreover intermediate expressions may be much bigger
than the input and output.
- OBJECTIVES.
- Our main interest will be here to study the implementation of algorithms
- that keep the swell of the intermediate expressions under control
- and offer optimal time complexity.
- Sine this is obviously a vast subject we will focus on
univariate polynomials, bivariate polynomials and matrix operations.
- But in fact these algorithms benefit to many other
Computer algebra algorithms.
- TYPICAL (TRIVIAL) EXAMPLE.
- Let
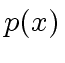 and
and 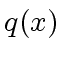 be two univariate polynomials
over the integer numbers and with degrees
be two univariate polynomials
over the integer numbers and with degrees 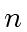 and
and 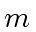 respectively such that
respectively such that 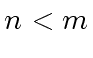 .
.
- Suppose we want to decide whether
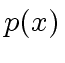 divides
divides 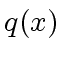 .
.
- One can show that the division with remainder of
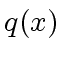 by
by
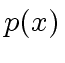 requires at most
requires at most
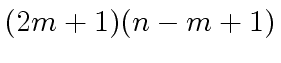 operations in the coefficient ring.
operations in the coefficient ring.
- If
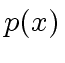 divides
divides 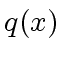 then for a given integer value
then for a given integer value 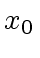 of
of 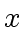 the integer
the integer 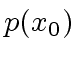 divides
divides 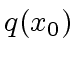 .
.
- Computing
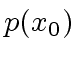 and
and 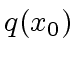 require
require
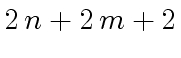 operations in the coefficient ring.
operations in the coefficient ring.
- So trying whether
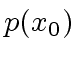 divides
divides 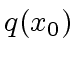 (before computing the remainder of
(before computing the remainder of 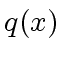 by
by 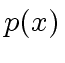 )
will save time (and space) in the average.
)
will save time (and space) in the average.
Marc Moreno Maza
2008-01-07
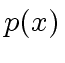 and
and 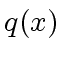 be two univariate polynomials
over the integer numbers and with degrees
be two univariate polynomials
over the integer numbers and with degrees 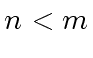 .
.
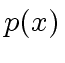 divides
divides 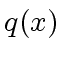 .
.
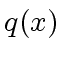 by
by
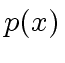 requires at most
requires at most
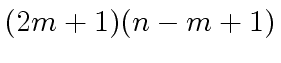 operations in the coefficient ring.
operations in the coefficient ring.
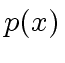 divides
divides 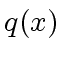 then for a given integer value
then for a given integer value 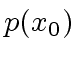 divides
divides 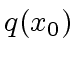 .
.
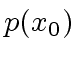 and
and 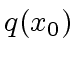 require
require
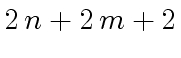 operations in the coefficient ring.
operations in the coefficient ring.
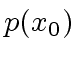 divides
divides 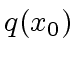 (before computing the remainder of
(before computing the remainder of 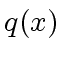 by
by 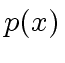 )
will save time (and space) in the average.
)
will save time (and space) in the average.