Next: A breif history Up: Computer Algebra Previous: Computer Algebra
By algebraic calculations we mean symbolic or exact computations.
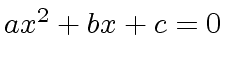 ,
,
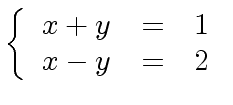 .
.
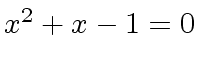 ,
,
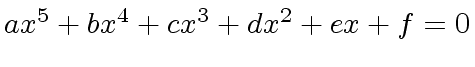 ,
,
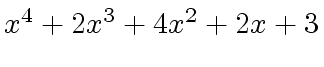 ,
,
Let us illustrate the question of exactness with an example. Consider the following system of 3 non-linear equations in 3 variable:
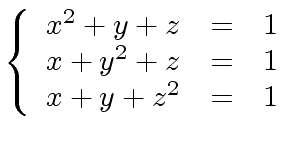 |
solution 1 : start residual : 3.968E-12 #iterations : 1 success x : 9.99999695984909E-01 4.13938269379988E-07 y : 3.04015091103714E-07 -4.13938269379988E-07 z : 3.04015090976779E-07 -4.13938269379988E-07 == err : 2.154E-06 = rco : 1.197E-07 = res : 9.920E-13 = complex regular == solution 2 : start residual : 1.388E-16 #iterations : 1 success x : 4.14213562373095E-01 2.35098870164458E-38 y : 4.14213562373095E-01 -1.67507944992176E-37 z : 4.14213562373095E-01 1.29304378590452E-37 == err : 7.517E-16 = rco : 6.017E-02 = res : 5.551E-17 = real regular == solution 3 : start residual : 2.400E-12 #iterations : 1 success x : 1.80048038888678E-08 4.29782537417684E-07 y : 9.99999981995196E-01 -4.29782537417684E-07 z : 1.80048038262633E-08 4.29782537417684E-07 == err : 1.344E-06 = rco : 7.463E-08 = res : 5.995E-13 = complex regular == solution 4 : start residual : 9.614E-13 #iterations : 1 success x : 1.00000024904061E+00 -3.93267692590196E-08 y : -2.49040612161639E-07 3.93267692590197E-08 z : -2.49040612108234E-07 3.93267692590197E-08 == err : 8.657E-07 = rco : 4.806E-08 = res : 2.400E-13 = complex regular == solution 5 : start residual : 2.745E-12 #iterations : 1 success x : 3.58839953269127E-07 1.89357516639334E-07 y : 3.58839953269127E-07 1.89357516639334E-07 z : 9.99999641160047E-01 -1.89357516639334E-07 == err : 1.645E-06 = rco : 7.071E-08 = res : 6.863E-13 = complex regular == solution 6 : start residual : 1.744E-34 #iterations : 1 success x : -2.41421356237309E+00 0.00000000000000E+00 y : -2.41421356237309E+00 0.00000000000000E+00 z : -2.41421356237309E+00 -1.00577224408752E-106 == err : 3.611E-35 = rco : 4.142E-01 = res : 6.868E-106 = real regular == solution 7 : start residual : 1.112E-12 #iterations : 1 success x : -2.64786238552867E-07 -4.67724648385200E-08 y : -2.64786238552867E-07 -4.67724648385200E-08 z : 1.00000026478624E+00 4.67724648385200E-08 == err : 9.341E-07 = rco : 4.530E-08 = res : 2.779E-13 = complex regular == solution 8 : start residual : 2.045E-12 #iterations : 1 success x : 1.42636460554469E-07 -3.16738323586431E-07 y : 9.99999857363539E-01 3.16738323586431E-07 z : 1.42636460467758E-07 -3.16738323586431E-07 == err : 1.378E-06 = rco : 7.656E-08 = res : 5.117E-13 = complex regular == =========================================================================== A list of 8 solutions has been refined : Number of regular solutions : 8. Number of singular solutions : 0. Number of real solutions : 2. Number of complex solutions : 6. Number of clustered solutions : 0. Number of failures : 0. ===========================================================================The solution provided by triade my symbolic solver in ALDOR is
{z^2 +2*z -1,
y -z,
x -z}
{z,
y -1,
x}
{z,
y,
x -1}
{z -1,
y,
x}
Dimensions: [0,0,0,0]
Degrees: [2,1,1,1]
How to choose between symbolic and numeric methods?
Marc Moreno Maza