Next: Multivariate polynomials. Up: How to encode the elements Previous: Real algebraic numbers.
Let ![]() be a ring. The univariate polynomial ring
be a ring. The univariate polynomial ring ![$ R[x]$](img156.png) can be implemented using different data types.
can be implemented using different data types.
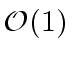 .
But the representation is not canonical:
two different expression trees can encode the same polynomial.
Therefore operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM
are in
.
But the representation is not canonical:
two different expression trees can encode the same polynomial.
Therefore operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM
are in
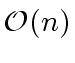 where
where 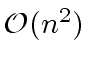 (for non-balanced trees).
(for non-balanced trees).
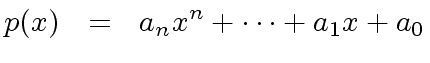 |
(34) |
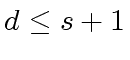 ,
,
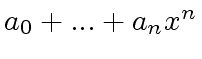 is represented by
is represented by
![$ [a_0,...,a_n,...]$](img194.png) and
and 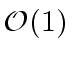 .
Addition and equality-test are in
.
Addition and equality-test are in
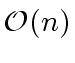 and multiplication
is in
and multiplication
is in
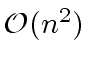 .
This representation is especially good when the ring of coefficients
is a small prime field, i.e.
.
This representation is especially good when the ring of coefficients
is a small prime field, i.e.
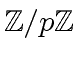 with
with ![$ [2, 2^{N} - 1]$](img186.png) .
.
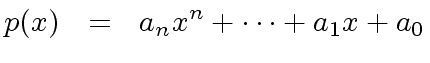 |
(35) |
![$ [a_i, i]$](img198.png) where
where 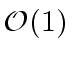 .
Moreover the operation REDUCTUM does not require
coefficient duplication (on the contrary of the previous
representation).
Addition and equality-test are in
.
Moreover the operation REDUCTUM does not require
coefficient duplication (on the contrary of the previous
representation).
Addition and equality-test are in
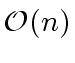 and multiplication
is in
and multiplication
is in
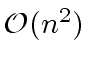 .
This representation is especially good when the ring of coefficients
is itself a ring of sparse polynomials.
.
This representation is especially good when the ring of coefficients
is itself a ring of sparse polynomials.
Marc Moreno Maza