Recall that the RINGS 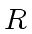 in Computer Algebra
are obtained by applying rules like
in Computer Algebra
are obtained by applying rules like
- (1)
-
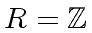 ,
,
- (2)
-
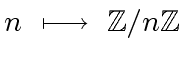 ,
,
- (3)
-
![$ R \ \longmapsto \ {R}[X]$](img211.png) ,
,
- (4)
-
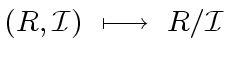
- (5)
-
 ,
,
- (6)
-
 .
.
To implement the above rules we would like to do the following constructions
in our programming language.
- To define functions which return a type (as in rule (2)).
- To define functions that can be parametrized by a type (as in rule (3)).
Hence we need GENERICITY.
- To handle INTERFACE (or type of types).
Indeed in (3) we need
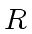 to be a ring.
Hence we need BOUNDED GENERICITY.
to be a ring.
Hence we need BOUNDED GENERICITY.
- In rule (4) we need to say that
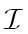 is an ideal of
is an ideal of 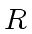 .
Hence we need BOUNDED GENERICITY
WITH DEPENDENT TYPES.
.
Hence we need BOUNDED GENERICITY
WITH DEPENDENT TYPES.
- We should be able to have functions as parameters of other functions.
For instance an ordered abelian free monoid genetated by
a set
 depends on a total ordering on
depends on a total ordering on  .
Hence functions must have types too.
Finally, both functions and types must
have types and must be possible parameters for functions.
Hence functions and types must
be TREATED AS VALUES.
.
Hence functions must have types too.
Finally, both functions and types must
have types and must be possible parameters for functions.
Hence functions and types must
be TREATED AS VALUES.
Marc Moreno Maza
2008-01-07
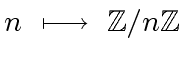 ,
,
![$ R \ \longmapsto \ {R}[X]$](img211.png) ,
,
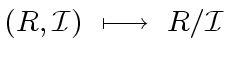
 ,
,
 .
.