Next: Symbolic Newton Iteration Up: Foundations of Computer Algebra: Symbolic Previous: Foundations of Computer Algebra: Symbolic
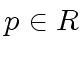 be a prime
element.
Let
be a prime
element.
Let  be an element.
We say that
be an element.
We say that 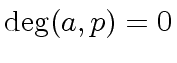 if for every positive integer
if for every positive integer
 the quotient of
the quotient of 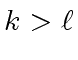 such that
the quotient of
such that
the quotient of  ,
otherwise we say that
,
otherwise we say that 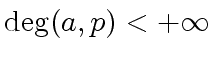 .
Assume furthermore that
.
Assume furthermore that
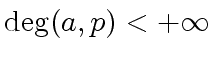 holds.
The largest positive integer
holds.
The largest positive integer
 such that the quotient of
such that the quotient of 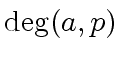 .
.
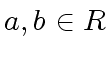 with
with
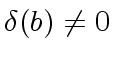 there exists a couple
there exists a couple
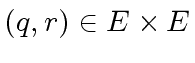 such that
such that
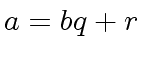 ,
,
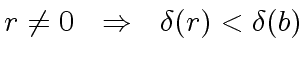 ,
,
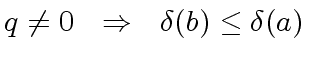 ,
,
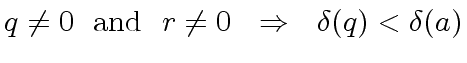 .
.
![$ k[x]$](img23.png) of univariate polynomials
over a field
of univariate polynomials
over a field
 there exists
an integer
there exists
an integer 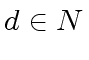 and elements
and elements
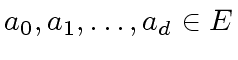 such that
such that
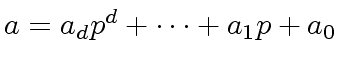 ,
,
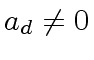 ,
,
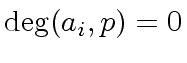 .
.
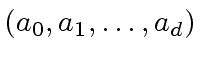 is called
a
is called
a
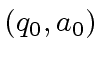 be a couple quotient-remainder
given as in
Definition 2
when dividing
be a couple quotient-remainder
given as in
Definition 2
when dividing
First we prove that ![]() must have degree 0
w.r.t.
must have degree 0
w.r.t. ![]() .
This is obvious if
.
This is obvious if 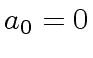 .
So let us assume that
.
So let us assume that
 holds.
This implies
holds.
This implies
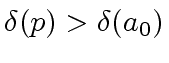 .
If
.
If ![]() would have positive degree
would have positive degree ![]() w.r.t.
w.r.t. ![]() ,
then, by the properties of a regular Euclidean size,
we would have
,
then, by the properties of a regular Euclidean size,
we would have
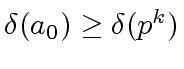 .
Since
.
Since
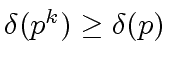 holds (by definition
of an Euclidean domain) we would have a contradiction
with
holds (by definition
of an Euclidean domain) we would have a contradiction
with
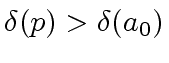 .
Therefore in any case we have
.
Therefore in any case we have
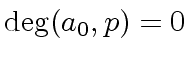 .
.
Next, let us prove the proposition for those elements ![]() which have quotient 0
w.r.t.
which have quotient 0
w.r.t. ![]() .
Observe that if one quotient of
.
Observe that if one quotient of ![]() w.r.t.
w.r.t. ![]() is zero
then we have
is zero
then we have
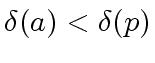 .
Hence every quotient of
.
Hence every quotient of ![]() w.r.t.
w.r.t. ![]() is null.
(Otherwise we would have
is null.
(Otherwise we would have
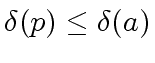 by the properties of a regular Euclidean size.)
Since
by the properties of a regular Euclidean size.)
Since 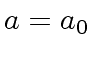 and since
and since ![]() has degree 0
w.r.t.
has degree 0
w.r.t. ![]() ,
the element
,
the element ![]() has degree 0
w.r.t.
has degree 0
w.r.t. ![]() and
and 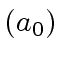 is a
is a ![]() -adic expansion of
-adic expansion of ![]() w.r.t.
w.r.t. ![]() .
Therefore the proposition is proved in the case
of the elements
.
Therefore the proposition is proved in the case
of the elements ![]() which have quotient 0
w.r.t.
which have quotient 0
w.r.t. ![]() .
.
We can assume now that ![]() does not have quotient 0
w.r.t.
does not have quotient 0
w.r.t. ![]() .
Then, two cases arise:
.
Then, two cases arise:
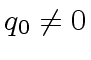 and
and
 hold,
and this case we have
hold,
and this case we have
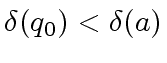 ;
then, we consider
;
then, we consider
 a couple quotient-remainder
given as in
Definition 2
when dividing
a couple quotient-remainder
given as in
Definition 2
when dividing 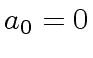 . Then, there exists a smallest integer
. Then, there exists a smallest integer 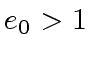 such that the remainder in an division of
such that the remainder in an division of 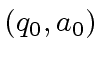 be a couple quotient-remainder
in an division of
be a couple quotient-remainder
in an division of  .
.
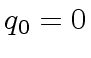 , then we stop.
, then we stop.
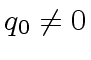 , then
, then
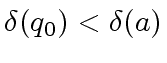 ;
then, we consider
;
then, we consider
 a couple quotient-remainder
given as in
Definition 2
when dividing
a couple quotient-remainder
given as in
Definition 2
when dividing  ,
we can repeat a similar discussion as we did for
,
we can repeat a similar discussion as we did for
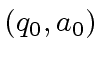 .
.
Continuing in this manner we obtain a finite sequence
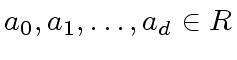 , a finite sequence
, a finite sequence
 and a finite sequence
and a finite sequence
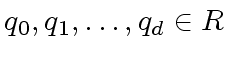 such that we have
such that we have
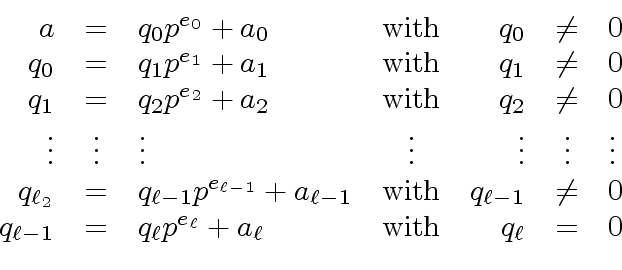 |
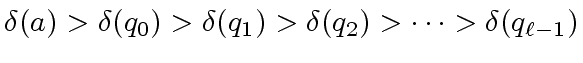 |
(1) |
 .
Clearly, there exitst
.
Clearly, there exitst
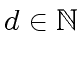 such that
such that 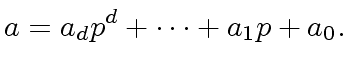 |
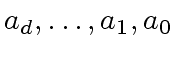 are null or have degree 0 w.r.t.
are null or have degree 0 w.r.t. 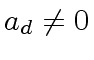 holds.
holds.
![$ {\bf k}[x]$](img61.png) of univariate polynomials
over a field
of univariate polynomials
over a field ![$ R[y]$](img63.png) of univariate polynomials
over an Euclidean domain
of univariate polynomials
over an Euclidean domain 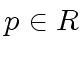 .
Indeed, one can apply
Proposition 1
to each coefficient of a polynomial
.
Indeed, one can apply
Proposition 1
to each coefficient of a polynomial
![$ {\phi} \in R[y]$](img64.png) .
.
As we shall see now, it extends to a ring
![$ R[y]$](img63.png) of univariate polynomials over a commutative ring
with identity element and to the element
of univariate polynomials over a commutative ring
with identity element and to the element 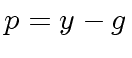 where
where ![]() is an element of
is an element of ![]() .
.
![$ {\phi} \in R[y]$](img64.png) be a polynomial of degree
be a polynomial of degree 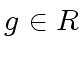 be an element.
We define
be an element.
We define 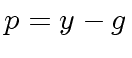 .
There exists a unique sequence
.
There exists a unique sequence
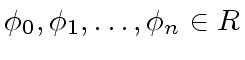 such that we have
such that we have
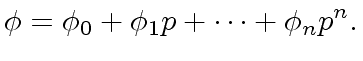 |
(2) |
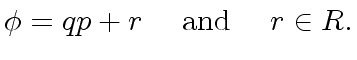 |
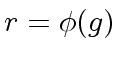 the conclusion
(existence and unicity) follows by the induction hypothesis.
the conclusion
(existence and unicity) follows by the induction hypothesis.
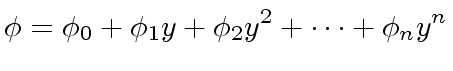 |
![$ {\phi}, {\psi} \in R[y]$](img79.png) and let
and let 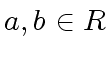 .
Then the following properties hold
.
Then the following properties hold
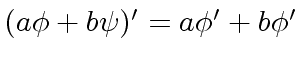 ,
,
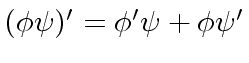 ,
,
 .
.
![$ {\phi} \in R[y]$](img64.png) and let
and let 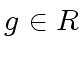 .
There exists a polynomial
.
There exists a polynomial
![$ {\psi} \in R[y]$](img83.png) such that we have
such that we have
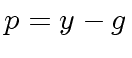 .
The division of
.
The division of 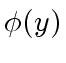 by
by  .
Similarly, from (Equation 3), we have
.
Similarly, from (Equation 3), we have
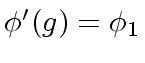 .
Plugging
.
Plugging
 and
and
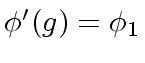 in
(Equation 5)
leads to
in
(Equation 5)
leads to
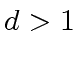 .
In this case the coefficients
.
In this case the coefficients
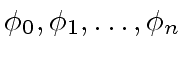 are polynomials of degree less than
are polynomials of degree less than ![$ {\phi} \in R[y,g]$](img94.png) .
.
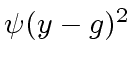 in Relation (4)
lies in the ideal
in Relation (4)
lies in the ideal
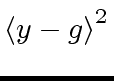 .
.
![$ P = R[x_1, \ldots, x_r][y_1, \ldots, y_r]$](img97.png) .
We define
.
We define
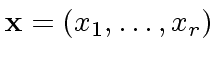 and
and
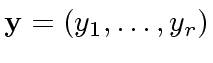 .
For every polynomial
.
For every polynomial
![$ {\phi} \in R[{\bf x}]$](img100.png) there exists a polynomial
there exists a polynomial
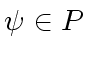 lying in the ideal
lying in the ideal
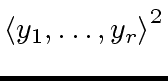 such that
such that
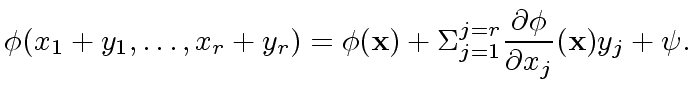 |
(7) |
 be elements and
be elements and 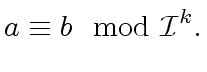 |
(8) |
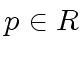 be a prime element.
Let
be a prime element.
Let 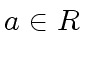 be an element and let
be an element and let
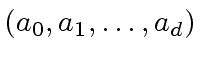 be a
be a 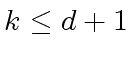 we define
we define
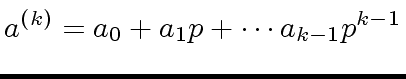 |
(9) |
 |
(10) |
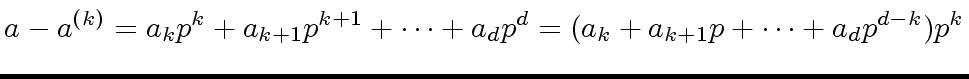 |
 be elements, let
be elements, let ![$ {\phi} \in R[y]$](img64.png) be a polynomial.
Then we have
be a polynomial.
Then we have
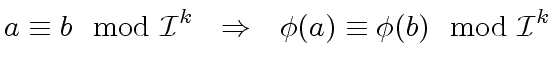 |
(11) |
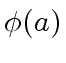 is an
is an 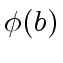 at order
at order
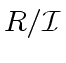 .
.
Marc Moreno Maza