Next: The resultant Up: Advanced Computer Algebra: The resultant Previous: Coefficients growth in the Euclidean
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img8.png) and
and
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) . Polynomial gcds in non Euclidean domains.
. Polynomial gcds in non Euclidean domains.
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) since
since
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) is not an Euclidean domain.
However the concept of a polynomial gcd is well defined in
is not an Euclidean domain.
However the concept of a polynomial gcd is well defined in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) since
since
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) is a Unique Factorization Domain, as we shall review.
is a Unique Factorization Domain, as we shall review.
If we transport the computation of a gcd from
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) to
to
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img8.png) we should be careful.
For instance with
we should be careful.
For instance with
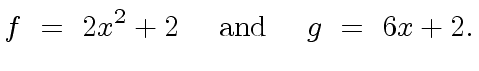 |
(11) |
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img8.png) their normalized gcd will be
their normalized gcd will be ![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) is 2.
is 2.
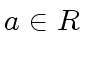 can be written
can be written
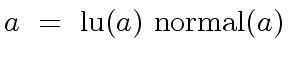 |
(12) |
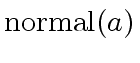 stands for a canonical representative
of the class of the elements associate with
stands for a canonical representative
of the class of the elements associate with 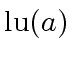 is a unit.
Observe that
is a unit.
Observe that 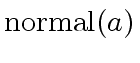 is
is
For
![]() we will take
we will take
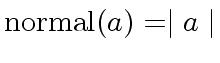 .
For
.
For
![$ R = {\bf k}[x]$](img56.png) we will take
we will take
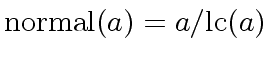 .
.
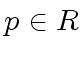 is reducible
if there are two nonunits
is reducible
if there are two nonunits 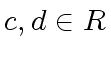 such that
such that
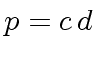 ,
otherwise
,
otherwise 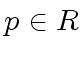 is prime if
for every
is prime if
for every 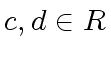 we have
we have
we have
we have
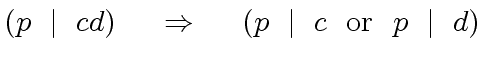 |
(13) |
Assume from now on that ![]() is a Unique Factorization Domain (UFD).
This means that
is a Unique Factorization Domain (UFD).
This means that ![]() is an integral domain such that
is an integral domain such that
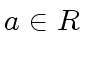 can be written as a product of irreducible elements
in a unique way up to reordering and multiplication by units.
can be written as a product of irreducible elements
in a unique way up to reordering and multiplication by units.
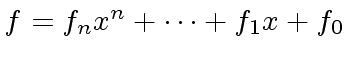 be a univariate polynomial over
be a univariate polynomial over  is the gcd of its coefficients
is the gcd of its coefficients
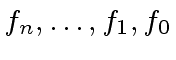 .
By convention the content of a constant polynomial
.
By convention the content of a constant polynomial 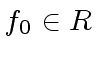 is
is
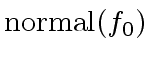 .
Observe that
.
Observe that
 is uniquely defined in any case.
is uniquely defined in any case.
The polynomial
![$ f \in R[x]$](img69.png) is primitive if
is primitive if
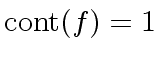 .
The primitive part of
.
The primitive part of
![$ f \in R[x]$](img69.png) is the polynomial
is the polynomial
![$ {\rm pp}(f) \in R[x]$](img71.png) such that
such that
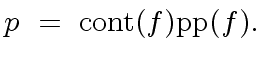 |
(14) |
![$ R[x]$](img75.png) is primitive.
is primitive.
![$ f,g \in R[x]$](img76.png) be primitive.
Let
be primitive.
Let 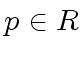 be a prime.
Then, the residue class ring
be a prime.
Then, the residue class ring 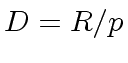 is an integral domain.
It follows (this is a classical result) that
is an integral domain.
It follows (this is a classical result) that ![$ D[x]$](img78.png) is an integral domain too.
By hypothesis
is an integral domain too.
By hypothesis 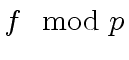 and
and 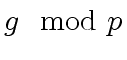 are not zero.
Hence
are not zero.
Hence
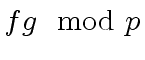 is not zero too.
This shows that
is not zero too.
This shows that 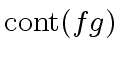 .
Finally we have proved that no primes divide
.
Finally we have proved that no primes divide
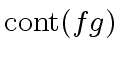 and thus
and thus
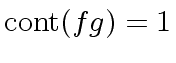 .
.
![$ f,g \in R[x]$](img76.png) .
Then we have
.
Then we have
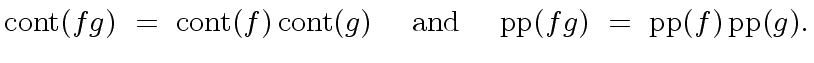 |
(16) |
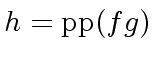 and
and
 .
By Gauss Lemma, the polynomial
.
By Gauss Lemma, the polynomial  |
(17) |
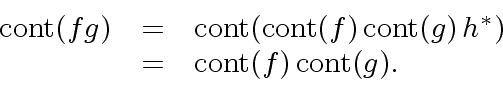 |
(18) |
![$ R[x_1, \ldots, x_n]$](img90.png) is a UFD.
is a UFD.
![$ f,g \in R[x]$](img76.png) be univariate polynomials over
be univariate polynomials over ![$ R[x]$](img75.png) .
Then the following properties hold.
.
Then the following properties hold.
![$ R[x]$](img75.png) are the primes of
are the primes of ![$ R[x]$](img75.png) that are irreducible in
that are irreducible in ![$ K[x]$](img93.png) .
.
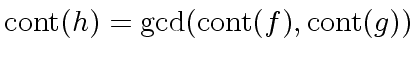 in
in 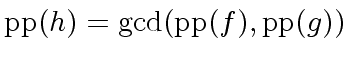 in
in ![$ R[x]$](img75.png) .
.
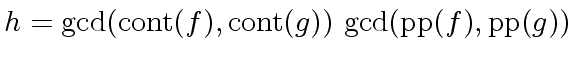
 is the monic gcd of
is the monic gcd of ![$ K[x]$](img93.png) .
.
![$ f,g \in R[x]$](img76.png) by means of a polynomial gcd computation
in
by means of a polynomial gcd computation
in ![$ K[x]$](img93.png) and gcd computations in
and gcd computations in 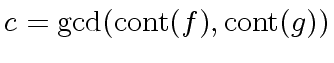 |
(19) |
![$ {\gcd}_{R[x]}(f,g)$](img100.png) we can assume that
we can assume that
![$ K[x]$](img93.png) .
We have
.
We have
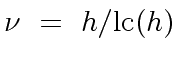 |
(20) |
![$ R[x]$](img75.png) then
then
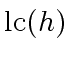 divides
divides
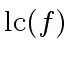 and
and
 in
in 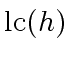 divides
divides
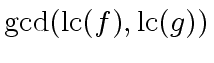 .
We define
.
We define
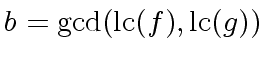 |
(21) |
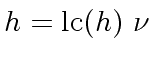 lies in
lies in ![$ R[x]$](img75.png) and since
and since
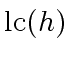 divides
divides ![$\displaystyle b \, {\nu} \in R[x]$](img109.png) |
(22) |
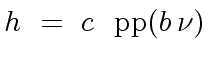 |
(23) |
![$ R[x_1, \ldots, x_n]$](img90.png) .
Of course this method based on the Euclidean Algorithm
may not be the most efficient one.
.
Of course this method based on the Euclidean Algorithm
may not be the most efficient one.
In fact for computing gcds in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) (and more generally
over
(and more generally
over
![$ {\mbox{${\mathbb{Z}}$}}[x_1, \ldots, x_n]$](img111.png) ) the modular methods (to be described
shortly) are much more efficient than going through
) the modular methods (to be described
shortly) are much more efficient than going through
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img8.png) and the Euclidean Algorithm.
and the Euclidean Algorithm.
The simplest approach would be
![$ {{\mbox{${\mathbb{Z}}$}}/{\langle p \rangle}}{\mbox{${\mathbb{Z}}$}}[x]$](img113.png) (rather than
(rather than
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) )
)
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) from
from
Marc Moreno Maza