Let
![$ f,g \in R[x]$](img76.png) be nonzero polynomials for an Euclidean domain
be nonzero polynomials for an Euclidean domain 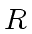 .
Let
.
Let 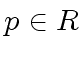 be a prime.
We denote by
be a prime.
We denote by
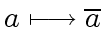 the reduction
modulo
the reduction
modulo 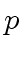 .
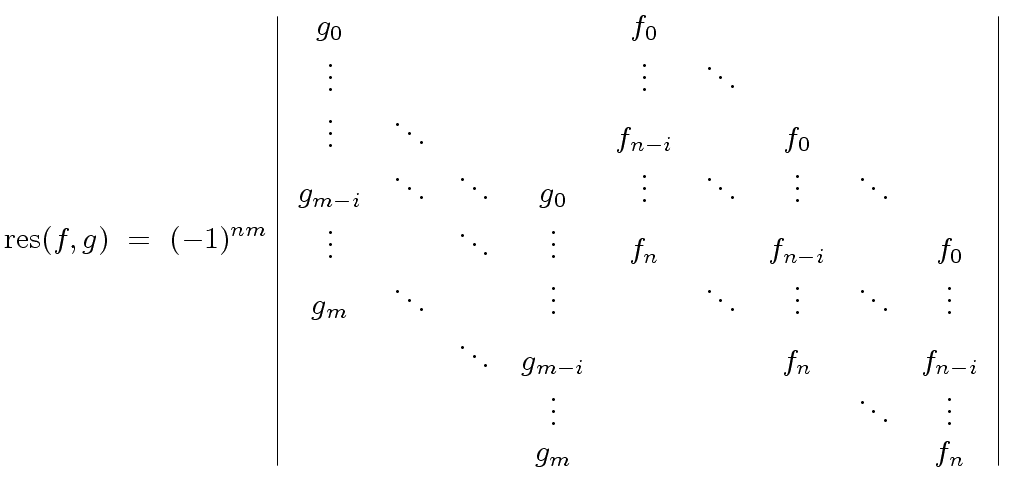
We know from the previous section that
.
We know from the previous section that
 |
(36) |
The formula of the resultant of 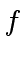 and
and 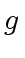 shows that
shows that
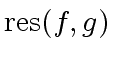 is a
multivariate polynomial expression in the coefficients of
is a
multivariate polynomial expression in the coefficients of 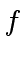 and
and 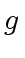 .
Hence we might be tempted to say
.
Hence we might be tempted to say
-
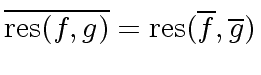 .
.
-
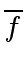 and
and
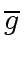 are coprime in
are coprime in ![$ R/p[x]$](img181.png) iff
iff 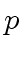 does not divide
does not divide
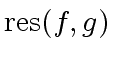 .
.
Proof.
Let us write:
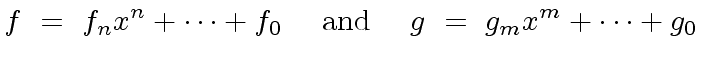 |
(44) |
with
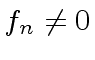
and
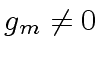
.
If
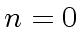
then
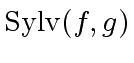
and
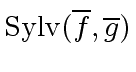
are both diagonal with
on the diagonal.
Then in that case
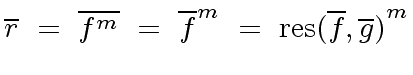 |
(45) |
If
we distinguish two cases.
If
then
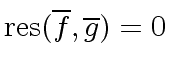
(by Definition
4).
Moreover each
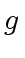
-column of
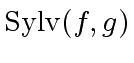
is zero modulo
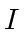
such that
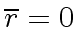
too.
From now on assume
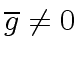
and let
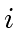
be the smallest index such that
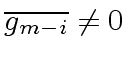
holds.
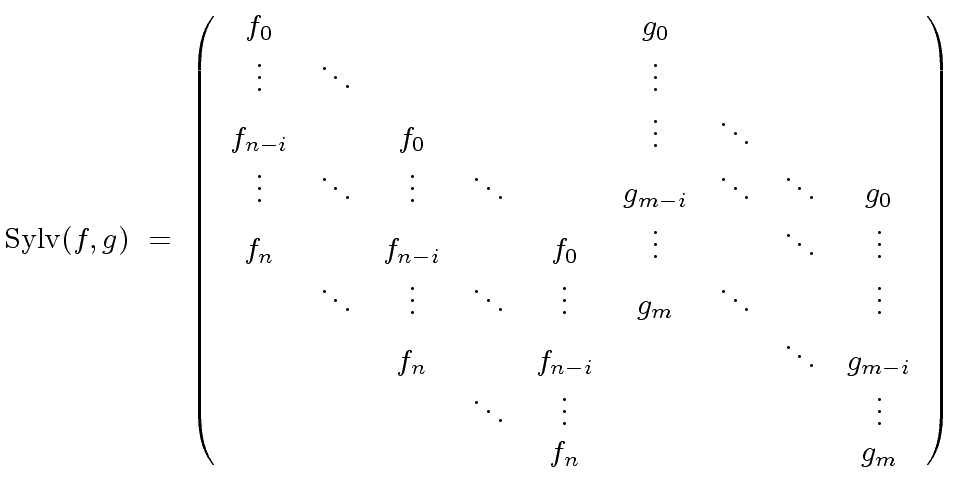 |
(46) |
By exchanging the
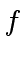
-
zone with the
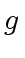
-
zone we have also
 |
(47) |
Let
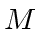
be the submatrix obtained from
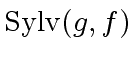
by deleting the
last
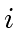
rows and the last
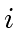
columns.
Observe that we have
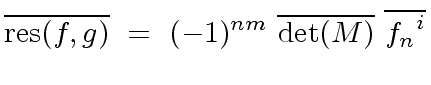 |
(48) |
Since
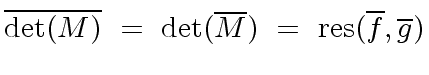 |
(49) |
we obtain
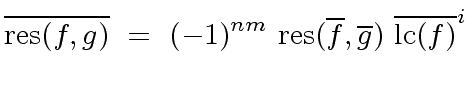 |
(50) |
This shows that we have
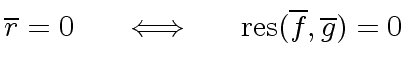 |
(51) |
and the first claim of the lemma is proved.
The second claim follows from
Proposition
6.

Proof.
Since in
![$ R[x]$](img75.png)
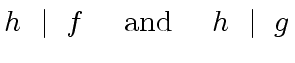 |
(55) |
we have in
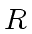
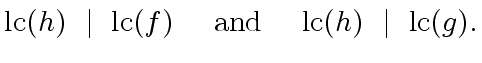 |
(56) |
Therefore
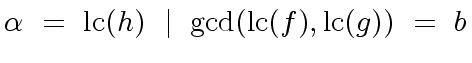 |
(57) |
and the first claim is proved.
Consider now the cofactors of
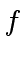
and
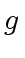
in
![$ R[x]$](img75.png)
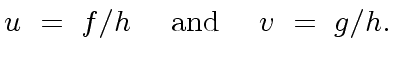 |
(58) |
Then we have
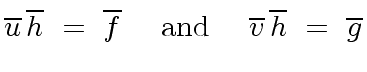 |
(59) |
which shows that
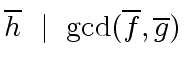 |
(60) |
and implies that
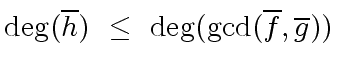 |
(61) |
Since
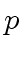
does not divide
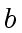
, it cannot not divide
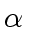
neither.
Hence the leading coefficient of
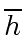
is
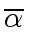
and we have
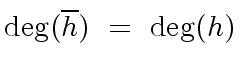 |
(62) |
Therefore
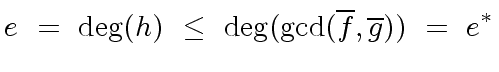 |
(63) |
and the second claim is proved.
Now consider the case where
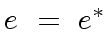 .
Since
.
Since
 divides
divides
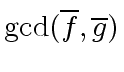 and since
and since
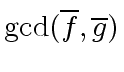 is monic (as a gcd over
the field
is monic (as a gcd over
the field 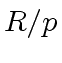 ) there exists a unit
) there exists a unit 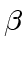 such that
such that
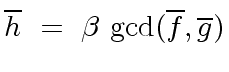 |
(64) |
Since the leading coefficient of
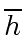
is
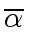
we have in fact
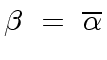 |
(65) |
Therefore we have the following equivalence
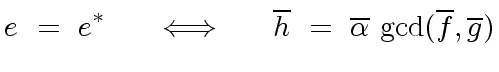 |
(66) |
It remains to prove that
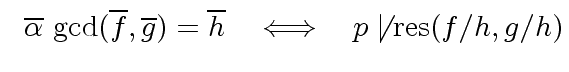 |
(67) |
Observe that
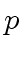
cannot divide both
and
.
If this was the case
then from Relation (
59) (and since
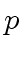
does not divide
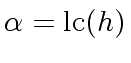
)
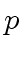
would divide
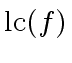
and
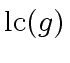
, and thus
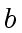
.
A contradiction. Therefore we can assume that
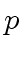
does not divide
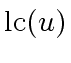
.
By applying Lemma
2 we obtain
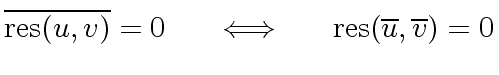 |
(68) |
By applying Proposition
5
this leads to
 |
(69) |
From Relation (
59) we have
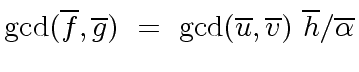 |
(70) |
Therefore
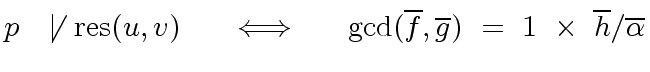 |
(71) |
This concludes the proof of the theorem.

Definition 5
Let
![$ f,g \in R[x]$](img76.png) be nonzero polynomials for an Euclidean domain
be nonzero polynomials for an Euclidean domain  .
Let
.
Let
![$ h \in R[x]$](img249.png) be
be
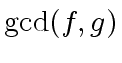 .
A prime element
.
A prime element 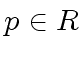 is said lucky if
is said lucky if 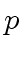 does not divide
does not divide
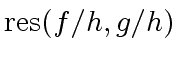 otherwise it is said unlucky.
otherwise it is said unlucky.
Example 2
Consider
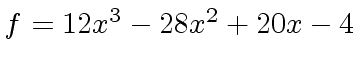 ,
,
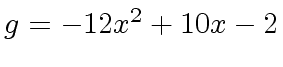 and
and 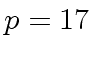 .
We have the following computation in AXIOM (where we do not display types)
.
We have the following computation in AXIOM (where we do not display types)
N := NonNegativeInteger
(1) NonNegativeInteger
Z := Integer
(2) Integer
U := UnivariatePolynomial(x,Z)
(3) UnivariatePolynomial(x,Integer)
f: U := 12*x^3 -28*x^2 +20*x - 4
3 2
(4) 12x - 28x + 20x - 4
g: U := -12*x^2 +10*x -2
2
(5) - 12x + 10x - 2
resultant(f,g)
(6) 0
h: U := gcd(f,g)
(7) 6x - 2
r: Z := resultant(exquo(f,h),exquo(g,h))
(8) 2
K17 := PrimeField(17)
(9) PrimeField 17
r :: K17
(10) 2
U17 := UnivariatePolynomial(x,K17)
(11) UnivariatePolynomial(x,PrimeField 17)
f17: U17 := f :: U17
3 2
(12) 12x + 6x + 3x + 13
g17: U17 := g :: U17
2
(13) 5x + 10x + 15
h17: U17 := h ::U17
(14) 6x + 15
c17 := gcd(f17,g17)
(15) x + 11
h17 - (leadingCoefficient(h17)) * c17
(16) 0
Example 3
Consider
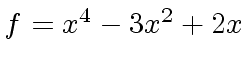 ,
,
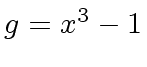 and
and 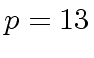 .
We have the following computation in AXIOM (where we do not display types)
The variables N, Z, U are defined as above.
.
We have the following computation in AXIOM (where we do not display types)
The variables N, Z, U are defined as above.
f: U := x^4 -3*x^3 + 2*x
4 3
(4) x - 3x + 2x
g: U := x^3 -1
3
(5) x - 1
resultant(f,g)
(6) 0
h: U := gcd(f,g)
(7) x - 1
r: Z := resultant(exquo(f,h),exquo(g,h))
(8) 9
K3 := PrimeField(3)
(9) PrimeField 3
r :: K3
(10) 0
U3 := UnivariatePolynomial(x,K3)
(11) UnivariatePolynomial(x,PrimeField 3)
f3: U3 := f :: U3
4
(12) x + 2x
g3: U3 := g :: U3
3
(13) x + 2
h3: U3 := h ::U3
(14) x + 2
c3 := gcd(f3,g3)
3
(15) x + 2
exquo(c3, h3)
2
(16) x + x + 1
Marc Moreno Maza
2008-01-07
![$ f,g \in R[x]$](img76.png) be nonzero polynomials for an Euclidean domain
be nonzero polynomials for an Euclidean domain ![]() .
Let
.
Let 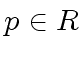 be a prime.
We denote by
be a prime.
We denote by
![]() the reduction
modulo
the reduction
modulo ![]() .
We know from the previous section that
.
We know from the previous section that

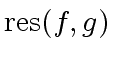 is a
multivariate polynomial expression in the coefficients of
is a
multivariate polynomial expression in the coefficients of 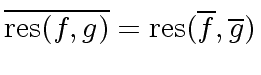 .
.
![$ R/p[x]$](img181.png) iff
iff 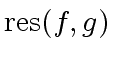 .
.
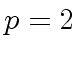 ,
, 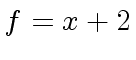 and
and 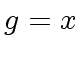 .
Then we have
.
Then we have
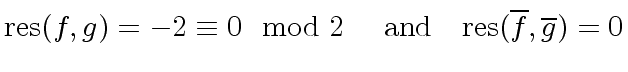
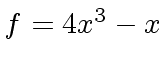 and
and
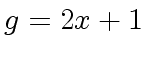 we have
we have
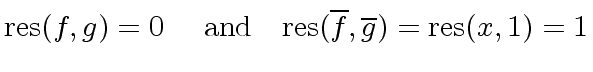
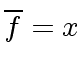 and
and
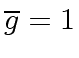 is
is

![$ f,g \in R[x]$](img76.png) be nonzero polynomials.
Let
be nonzero polynomials.
Let 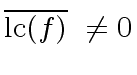
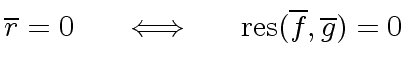
 is a UFD, then we have
is a UFD, then we have
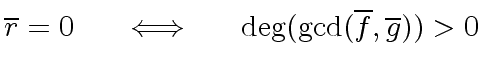
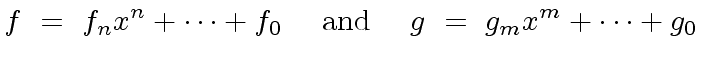
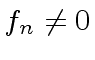 and
and
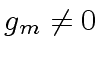 .
If
.
If 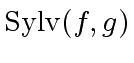 and
and
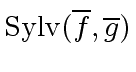 are both diagonal with
are both diagonal with 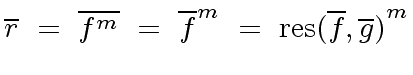
 we distinguish two cases.
If
we distinguish two cases.
If
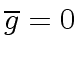 then
then
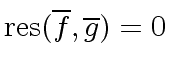 (by Definition 4).
Moreover each
(by Definition 4).
Moreover each 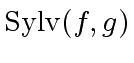 is zero modulo
is zero modulo 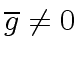 and let
and let 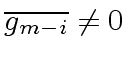 holds.
holds.
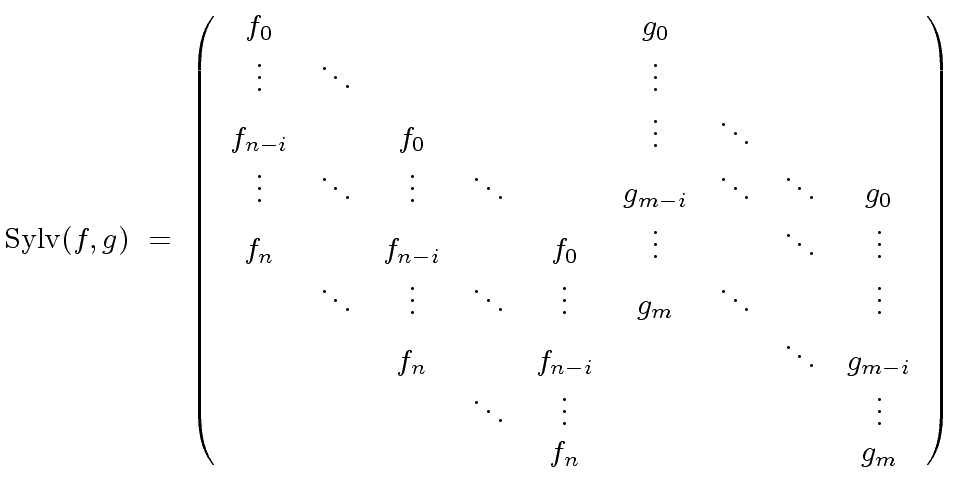

 by deleting the
last
by deleting the
last 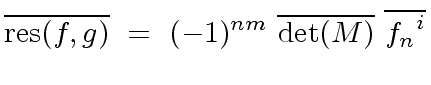
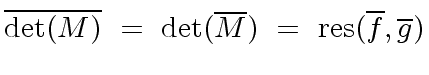
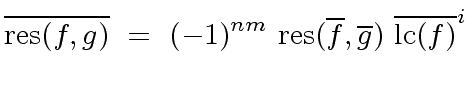
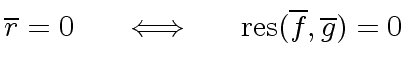
![$ f,g \in R[x]$](img76.png) be nonzero polynomials for an Euclidean Domain
be nonzero polynomials for an Euclidean Domain  be a prime.
Let
be a prime.
Let
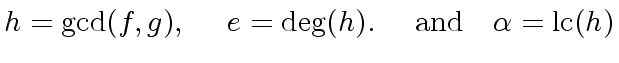
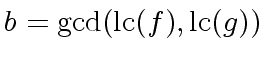
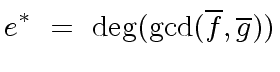
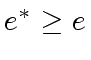
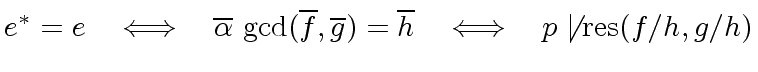
![$ R[x]$](img75.png)
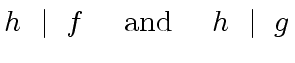
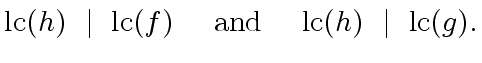
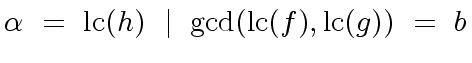
![$ R[x]$](img75.png)
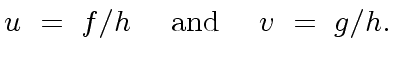
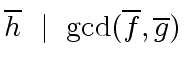
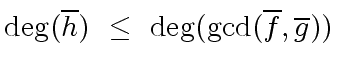
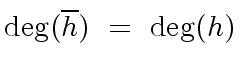
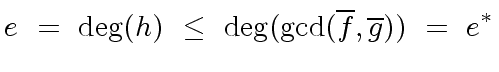
![]() .
Since
.
Since
![]() divides
divides
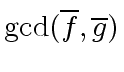 and since
and since
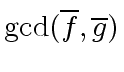 is monic (as a gcd over
the field
is monic (as a gcd over
the field 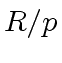 ) there exists a unit
) there exists a unit ![]() such that
such that
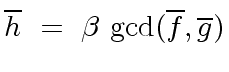
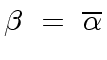
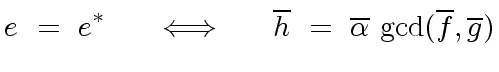
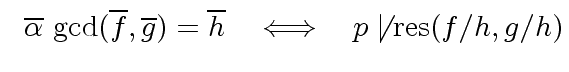
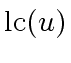 and
and
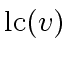 .
If this was the case
then from Relation (59) (and since
.
If this was the case
then from Relation (59) (and since
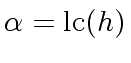 )
)
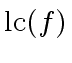 and
and
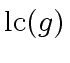 , and thus
, and thus 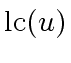 .
By applying Lemma 2 we obtain
.
By applying Lemma 2 we obtain
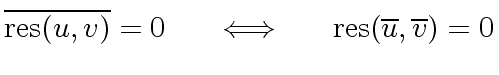

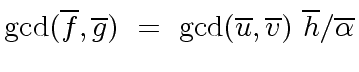
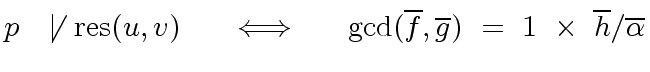
![$ f,g \in R[x]$](img76.png) be nonzero polynomials for an Euclidean domain
be nonzero polynomials for an Euclidean domain ![$ h \in R[x]$](img249.png) be
be
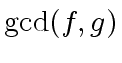 .
A prime element
.
A prime element 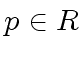 is said lucky if
is said lucky if 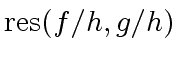 otherwise it is said unlucky.
otherwise it is said unlucky.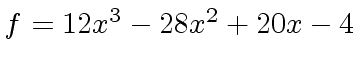 ,
,
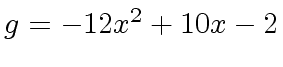 and
and 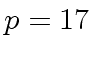 .
We have the following computation in AXIOM (where we do not display types)
.
We have the following computation in AXIOM (where we do not display types)
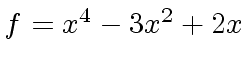 ,
,
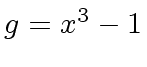 and
and 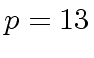 .
We have the following computation in AXIOM (where we do not display types)
The variables N, Z, U are defined as above.
.
We have the following computation in AXIOM (where we do not display types)
The variables N, Z, U are defined as above.