

Next: Bibliography
Up: Efficient implementation
Previous: Efficient implementation
We first change the intermediate polynomials.
Let n = 2r
mathend000# be a power of 2
mathend000#, let
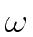
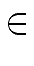 R
mathend000# be a primitive n
mathend000#-th
root of unity and
A(x) =
R
mathend000# be a primitive n
mathend000#-th
root of unity and
A(x) = 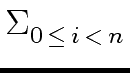 ai xi
mathend000#.
We define
ai xi
mathend000#.
We define
| A[0](x) |
= |
a0 + a2x + a4x2 + ... + an-2xn/2-1 |
| A[1](x) |
= |
a1 + a3x + a5x2 + ... + an-1xn/2-1 |
|
(55) |
such that we have
| A(x) = A[0](x2) + x A[1](x2). |
(56) |
Hence evaluating A
mathend000# at
1,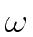 ,
,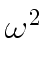 ,...,
,...,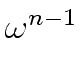 mathend000#
is reduced to evaluate A[0]
mathend000# and A[1]
mathend000# at
1,
mathend000#
is reduced to evaluate A[0]
mathend000# and A[1]
mathend000# at
1,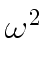 ,
,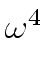 ,...,
,...,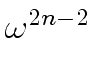 mathend000#.
But this second sequence of powers of
mathend000#.
But this second sequence of powers of 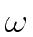 mathend000# consists
of two identical sequences of length n/2
mathend000#.
Indeed, for every integer k
mathend000# we have
mathend000# consists
of two identical sequences of length n/2
mathend000#.
Indeed, for every integer k
mathend000# we have
(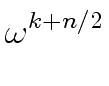 )2 = ( )2 = (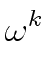 )2 )2 |
(57) |
Since
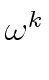 (1 -
(1 - 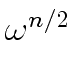 )
) 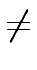 0
mathend000# holds, we obtain
0
mathend000# holds, we obtain
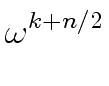 = - = - 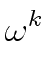 |
(58) |
Hence we only need to evaluate A[0]
mathend000# and A[1]
mathend000# at
This provides us directly with the values of A
mathend000# at
and the values of A
mathend000# at
by using the fact these numbers are respectively equal to
To summarize, for
0  i
i  n/2 - 1
mathend000# we have
n/2 - 1
mathend000# we have
A(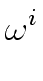 ) ) |
= |
A[0](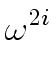 ) + ) + 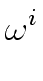 A[1]( A[1](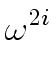 ) ) |
A(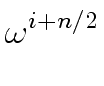 ) ) |
= |
A[0](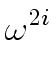 ) - ) - 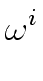 A[1]( A[1](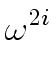 ) ) |
|
(63) |
Algorithm 3
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $n = 2^r$...
...n/2}$\ := $y_k^{[0]} - t$\ \\
\> {\bf return} $y$
\end{tabbing}\end{minipage}}](img143.png) mathend000#
mathend000#
The validity of Algorithm 3
follows from the two following observations.
- Formulas (63).
- If
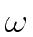 mathend000# is a primitive 2s
mathend000#-root of unity, with s > 1
mathend000#,
then
mathend000# is a primitive 2s
mathend000#-root of unity, with s > 1
mathend000#,
then
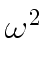 mathend000# is a primitive 2s-1
mathend000#-root of unity.
mathend000# is a primitive 2s-1
mathend000#-root of unity.
Observe that the recursive calls of
DFT(n, A,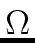 )
mathend000# defines
an ordering of the coefficients of A
mathend000# shown
on Figure 2 for n = 8
mathend000#.
Let us call this ordering the DFT ordering of A
mathend000#.
)
mathend000# defines
an ordering of the coefficients of A
mathend000# shown
on Figure 2 for n = 8
mathend000#.
Let us call this ordering the DFT ordering of A
mathend000#.
Observe that if the input array A
mathend000# is sorted w.r.t. this
DFT ordering, one can describe easily the
recursive calls with a binary tree.
If this tree is traversed bottom-up, from left to right,
we are led to an iterative algorithm working in place!
For instance, for n = 8
mathend000#, assuming that the input array A
mathend000# is
| | a0 | a4 | a2 | a6 | a1 | a5 | a3 | a7 | |
|
We obtain the desired result in A
mathend000# using the following straigth-line program
- a
mathend000# := a0
mathend000#
- b
mathend000# := a1
mathend000#
- a0
mathend000# := a + b
mathend000#
- a1
mathend000# := a - b
mathend000#
- a
mathend000# := a2
mathend000#
- b
mathend000# := a3
mathend000#
- a2
mathend000# := a + b
mathend000#
- a3
mathend000# := a - b
mathend000#
- a
mathend000# := a4
mathend000#
- b
mathend000# := a5
mathend000#
- a4
mathend000# := a + b
mathend000#
- a5
mathend000# := a - b
mathend000#
- a
mathend000# := a6
mathend000#
- b
mathend000# := a7
mathend000#
- a6
mathend000# := a + b
mathend000#
- a7
mathend000# := a - b
mathend000#
- a
mathend000# := a0
mathend000#
- b
mathend000# := a1
mathend000#
- c
mathend000# := a2
mathend000#
- d
mathend000# := a3
mathend000#
- a0
mathend000# := a + c
mathend000#
- a2
mathend000# := a - c
mathend000#
- a1
mathend000# :=
b +
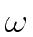 d
mathend000#
d
mathend000#
- a3
mathend000# :=
b -
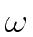 d
mathend000#
d
mathend000#
- a
mathend000# := a4
mathend000#
- b
mathend000# := a5
mathend000#
- c
mathend000# := a6
mathend000#
- d
mathend000# := a7
mathend000#
- a0
mathend000# := a + c
mathend000#
- a2
mathend000# := a - c
mathend000#
- a1
mathend000# :=
b +
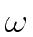 d
mathend000#
d
mathend000#
- a3
mathend000# :=
b -
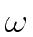 d
mathend000#
d
mathend000#
- a
mathend000# := a0
mathend000#
- b
mathend000# := a1
mathend000#
- c
mathend000# := a2
mathend000#
- d
mathend000# := a3
mathend000#
- e
mathend000# := a4
mathend000#
- f
mathend000# := a5
mathend000#
- g
mathend000# := a6
mathend000#
- h
mathend000# := a7
mathend000#
- a0
mathend000# := a + e
mathend000#
- a1
mathend000# :=
b +
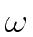 f
mathend000#
f
mathend000#
- a2
mathend000# :=
c +
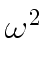 f
mathend000#
f
mathend000#
- a3
mathend000# :=
d +
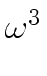 h
mathend000#
h
mathend000#
- a4
mathend000# := a + e
mathend000#
- a5
mathend000# :=
b -
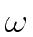 f
mathend000#
f
mathend000#
- a6
mathend000# :=
c -
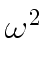 f
mathend000#
f
mathend000#
- a7
mathend000# :=
d -
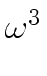 h
mathend000#
h
mathend000#
Figure 2:
Recursive calls for n = 8
mathend000#.
![\begin{figure}\htmlimage
\centering
\includegraphics[scale=.5]{fft8.eps}\end{figure}](img146.png) |
Algorithm 4
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] $n = 2^r$...
...k + j + m/2]$\ := $u - t$\ \\
\> {\bf return} $A$
\end{tabbing}\end{minipage}}](img147.png) mathend000#
mathend000#
Remark 8
To get the DFT ordering for A
mathend000#,
that is
[a0, a4, a2, a6, a1, a5, a3, a7]
mathend000#,
observe that this ordering changes
| 000, 001, 010, 011, 100, 101, 011, 111 |
(64) |
to
| 000, 100, 010, 110, 001, 101, 110, 111 |
(65) |
Remark 9
The ring
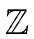 mathend000# does not have any interesting roots of unity.
In order to take advantage of the FFT-based multiplication
one could use a modular approach as follows.
mathend000# does not have any interesting roots of unity.
In order to take advantage of the FFT-based multiplication
one could use a modular approach as follows.
- Let f
mathend000# and g
mathend000# be two univariate polynomials in
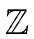 [x]
mathend000#.
We can assume that all their coefficients are positive.
Otherwise, we can restrict to this case by setting
[x]
mathend000#.
We can assume that all their coefficients are positive.
Otherwise, we can restrict to this case by setting
| f = f+ - f- and g = g+ - g- |
(66) |
where f+
mathend000#, f-
mathend000#, g+
mathend000#, g-
mathend000# are polynomials with positive coefficients
and writing
| f g = f+g+ + f-g- - f+g- - f-g+ |
(67) |
and computing the products
f+g+
mathend000#,
f-g-
mathend000#, f+g-
mathend000# and f-g+
mathend000#
one after another.
- Let
| | f | |
mathend000# and
| | g | |
mathend000#
be the max-norms of f
mathend000# and g
mathend000#.
Let d
mathend000# be the degree of f g
mathend000#.
For
k = 0 ... d
mathend000# a bound for the coefficient ck
mathend000# of xk
mathend000#
in f g
mathend000# is given by
| ck | 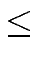 (k + 1) | | f | | | | g | | (k + 1) | | f | | | | g | | |
(68) |
- Let M
mathend000# be the biggest value of these bounds.
Let
p1,..., pr
mathend000# be primes such
- 2d
mathend000# divides each
p1 -1,..., pr - 1
mathend000#
- the product of
p1,..., pr
mathend000# is bigger than 2 M
mathend000#.
- Then we can compute f g
mathend000# in each of the
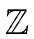 /pi
/pi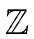 [x]
mathend000#
using the FFT-based multiplication.
[x]
mathend000#
using the FFT-based multiplication.
- Finally we can recombine these modular product by
applying the CRA to each coefficient ck
mathend000# (of xk
mathend000#) in f g
mathend000#.


Next: Bibliography
Up: Efficient implementation
Previous: Efficient implementation
Marc Moreno Maza
2007-01-10
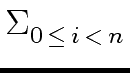 ai xi
ai xi
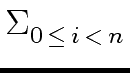 ai xi
ai xi
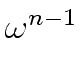
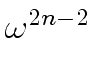
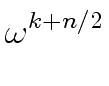 )2 = (
)2 = (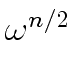 )
) 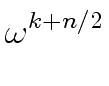 = -
= - 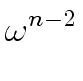 .
.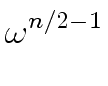
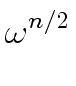 ,
,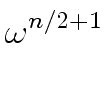 ,...,
,...,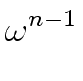
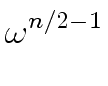 .
.