

Next: Rational numbers.
Up: How to encode the elements
Previous: How to encode the elements
One machine word can contain a SINGLE PRECISION
INTEGER in the range
[0, 2N - 1]
mathend000#.
To represent integers outside of this range, so called
MULTIPRECISION INTEGER, we use arrays of N
mathend000#-bit words.
To be precise we consider the 2N
mathend000#-ary (or radix 2N
mathend000#)
expansion of a nonzero integer:
a = (- 1)s 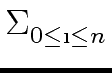 ai2Ni ai2Ni |
(33) |
where
- every
ai
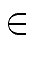 [0, 2N - 1]
mathend000# is a digit in
the 2N
mathend000#-ary expansion of a
mathend000#,
[0, 2N - 1]
mathend000# is a digit in
the 2N
mathend000#-ary expansion of a
mathend000#,
-
s
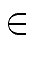 {0, 1}
mathend000# determines the sign of a
mathend000#,
{0, 1}
mathend000# determines the sign of a
mathend000#,
-
n + 1
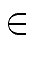 [1, 2N]
mathend000# is the number of 2N
mathend000#-digits in
the 2N
mathend000#-ary expansion of a
mathend000#,
[1, 2N]
mathend000# is the number of 2N
mathend000#-digits in
the 2N
mathend000#-ary expansion of a
mathend000#,
-
an
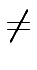 0
mathend000#.
0
mathend000#.
Then the integer a
mathend000# with (n + 1)
mathend000# 2N
mathend000#-digits
can be represented by an array (of N
mathend000#-bit words)
with length n + 3
mathend000# since we need
- one word for s
mathend000# and
- one word for n
mathend000#
The reasonable UNIT OPERATION for integers
is the the WORD OPERATION.
One can easily check that
- the ADDITION of two integers with
at most n
mathend000# 2N
mathend000#-digits requires
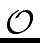 (n)
mathend000# word operations
(n)
mathend000# word operations
- the MULTIPLICATION of two integers with
at most n
mathend000# 2N
mathend000#-digits requires
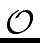 (n2)
mathend000# word operations.
(n2)
mathend000# word operations.


Next: Rational numbers.
Up: How to encode the elements
Previous: How to encode the elements
Marc Moreno Maza
2007-01-10
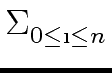 ai2Ni
ai2Ni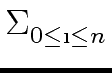 ai2Ni
ai2Ni