

Next: Multivariate polynomials.
Up: How to encode the elements
Previous: Real algebraic numbers.
Let R
mathend000# be a ring. The univariate polynomial ring R[x]
mathend000#
can be implemented using different data types.
- Expression trees.
- All arithmetic operations are in
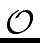 (1)
mathend000#.
But the representation is not canonical:
two different expression trees can encode the same polynomial.
Therefore operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM
are in
(1)
mathend000#.
But the representation is not canonical:
two different expression trees can encode the same polynomial.
Therefore operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM
are in
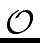 (n)
mathend000# where n
mathend000# is the degree of the polynomial.
Even worst the equality-test is
(n)
mathend000# where n
mathend000# is the degree of the polynomial.
Even worst the equality-test is
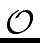 (n2)
mathend000# (for non-balanced trees).
(n2)
mathend000# (for non-balanced trees).
- Arrays of coefficients.
- The polynomial
| p(x) = anxn + ... + a1x + a0 |
(34) |
is coded by a record consisting of
- a single integer s
mathend000#,
- a single integer
d
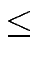 s + 1
mathend000#,
s + 1
mathend000#,
- an array of size s
mathend000# such that
a0 + ... + anxn
mathend000# is represented by
[a0,..., an,...]
mathend000#
and d = n
mathend000#.
This representation is said dense
becasue all ai
mathend000# are coded, even those which are null.
This representation is canonical.
Hence operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM are in
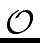 (1)
mathend000#.
Addition and equality-test are in
(1)
mathend000#.
Addition and equality-test are in
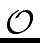 (n)
mathend000# and multiplication
is in
(n)
mathend000# and multiplication
is in
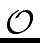 (n2)
mathend000#.
This representation is especially good when the ring of coefficients
is a small prime field, i.e.
(n2)
mathend000#.
This representation is especially good when the ring of coefficients
is a small prime field, i.e.
 /p
/p mathend000# with p
mathend000# prime and
in the range
[2, 2N - 1]
mathend000#.
mathend000# with p
mathend000# prime and
in the range
[2, 2N - 1]
mathend000#.
- List of terms.
- The polynomial
| p(x) = anxn + ... + a1x + a0 |
(35) |
is coded by the list L
mathend000# of records [ai, i]
mathend000#
where ai
mathend000# is a nonzero coefficient
and such that L
mathend000# is sorted decreasingly w.r.t. i
mathend000#.
This representation is said sparse,
since only the nonzero ai
mathend000# are coded.
This representation is also canonical.
Hence operations like DEGREE, LEADING COEFFICIENT,
REDUCTUM are in
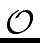 (1)
mathend000#.
Moreover the operation REDUCTUM does not require
coefficient duplication (on the contrary of the previous
representation).
Addition and equality-test are in
(1)
mathend000#.
Moreover the operation REDUCTUM does not require
coefficient duplication (on the contrary of the previous
representation).
Addition and equality-test are in
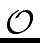 (n)
mathend000# and multiplication
is in
(n)
mathend000# and multiplication
is in
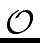 (n2)
mathend000#.
This representation is especially good when the ring of coefficients
is itself a ring of sparse polynomials.
(n2)
mathend000#.
This representation is especially good when the ring of coefficients
is itself a ring of sparse polynomials.


Next: Multivariate polynomials.
Up: How to encode the elements
Previous: Real algebraic numbers.
Marc Moreno Maza
2007-01-10
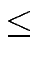 s + 1
s + 1