

Next: Asymptotically fast algorithms
Up: What are our requirements for
Previous: Post-facto extensions
In any MONOID exponentiation can de defined by the binary powering
algorithm
(^)(x: %, n: NonNegativeInteger): % ==
(n < 0) =>
error "power: negative exponent";
n = 0 => 1;
n = 1 => x;
n = 2 => x*x;
-- General code.
i: SingleInteger := 0;
l: SingleInteger := length n;
u: % := 1;
repeat {
if bit(n, i) then u := u * x;
if i >= l then break;
x := x * x;
i := i + 1;
}
u
}
Assume that in the interface MONOID the exponentiation
has been defined as above.
In the MONOID
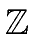 /p
/p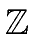 mathend000# (where p
mathend000# is a prime)
we can do better because of little Fermat theorem
which states that for x
mathend000# (where p
mathend000# is a prime)
we can do better because of little Fermat theorem
which states that for x 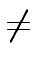 0
mathend000# we have
xp-1 = 1
mathend000#.
Hence we need to overwrite the above definition
for
0
mathend000# we have
xp-1 = 1
mathend000#.
Hence we need to overwrite the above definition
for
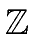 /p
/p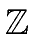 mathend000# by something like
mathend000# by something like
(^)(x: %, n: NonNegativeInteger): % == {
n := positiveRemainder(n,p);
zero? n => 1;
one? x => x;
local acc: %;
if odd? n then acc := x else acc := 1;
repeat {
n := shift(n,-1);
zero? n => return acc;
x := (x * x) mod p;
if odd? n then acc := (acc * x) mod p;
}
}
This will be made possible by INHERITANCE.
In a polynomial ring R[x]
mathend000# one can do better too in some
special cases depending on the coefficient ring, as we have seen before.
This will be made possible by CONDITIONAL IMPLEMENTATION.


Next: Asymptotically fast algorithms
Up: What are our requirements for
Previous: Post-facto extensions
Marc Moreno Maza
2007-01-10