
Next: Experimentation
Up: Asymptotically fast algorithms
Previous: Asymptotically fast algorithms
Let f, g
mathend000# be two univariate polynomials in x
mathend000# with degrees
p
mathend000# and q
mathend000# respectively.
Let
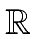 mathend000# be their ring of coefficients.
Define
mathend000# be their ring of coefficients.
Define
| f (x) = apxp + ... + a1x + a0 |
(39) |
and
| g(x) = bqxq + ... + b1x + b0. |
(40) |
COMPUTING THE PRODUCT f (x)g(x)
mathend000# by the straightforward method requires
-
(p + 1)(q + 1)
mathend000# multiplications in
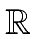 mathend000# and
mathend000# and
- pq
mathend000# additions in
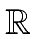 mathend000#.
mathend000#.
So the complexity of this computation is
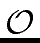 (pq)
mathend000#
(in term of operations in
(pq)
mathend000#
(in term of operations in
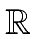 mathend000#).
mathend000#).
Thus the complexity of the computation of the product
of two univariate polynomials of degree at most n
mathend000#
is
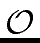 (n2)
mathend000# (in term of operations in
(n2)
mathend000# (in term of operations in
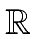 mathend000#).
mathend000#).
COMPUTING THE SUM
f (x) + g(x)
mathend000#
is
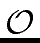 (n)
mathend000# (in term of operations in
(n)
mathend000# (in term of operations in
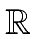 mathend000#)
if f
mathend000# and g
mathend000# have of degree at most n
mathend000#.
mathend000#)
if f
mathend000# and g
mathend000# have of degree at most n
mathend000#.
ADDING IS OFTEN CHEAPER THAN MULTIPLYING.
So adding polynomials is cheaper than multiplying them.
For many rings
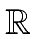 mathend000# addition is also cheaper than multiplication.
So when computing f (x)g(x)
mathend000# let's try to save on the number of
multiplications in
mathend000# addition is also cheaper than multiplication.
So when computing f (x)g(x)
mathend000# let's try to save on the number of
multiplications in
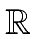 mathend000#.
mathend000#.
THE KARATSUBA'S TRICK.
Assume f
mathend000# and g
mathend000# have degree
(strictly) less than n = 2k
mathend000# (where k
mathend000# is an integer).
The Karatsuba's trick computes the product f (x)g(x)
mathend000# as follows.
- (1)
mathend000#
- If n = 1
mathend000# then compute the element f g
mathend000# of
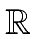 mathend000#.
mathend000#.
- (2)
mathend000#
- Define
f = F1 xn/2 + F0
mathend000# and
g = G1 xn/2 + G0
mathend000#
where
F1, F0, G1, G0
mathend000# have degree < n/2
mathend000#.
- (3)
mathend000#
- Compute
F0 G0
mathend000#,
F1 G1
mathend000#,
(F0 + F1)(G0 + G1)
mathend000# recursively
- (4)
mathend000#
- Return
F1G1 xn + 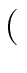 (F0 + F1)(G0 + G1) - F0 G0 - F1 G1 (F0 + F1)(G0 + G1) - F0 G0 - F1 G1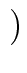 xn/2 + F0 G0. xn/2 + F0 G0. |
(41) |
ITS COMPLEXITY.
Let us count how many operations in
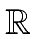 mathend000# we perform with the Karatsuba's trick.
mathend000# we perform with the Karatsuba's trick.
- At step (3)
mathend000# we perform at most n
mathend000# additions to compute
(F0 + F1)
mathend000# and
(G0 + G1)
mathend000#.
- At step (4)
mathend000# we perform at most 2 n
mathend000# subtractions to compute
(F0 + F1)(G0 + G1) - F0 G0 - F1 G1
mathend000#
- At step (5)
mathend000# we perform at most n
mathend000# additions to add this latter polynomial
to
F1G1 xn + F0 G0
mathend000#.
Hence we can apply the previous formula (for estimating T(n)
mathend000#) with
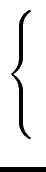 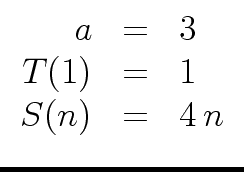 |
(42) |
We obtain
T(n) 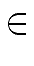 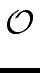 (4 n nlog2(3)-1). (4 n nlog2(3)-1). |
(43) |
that is
T(n) 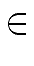 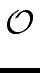 (nlog2(3)). (nlog2(3)). |
(44) |
Observe that:
log2(3) 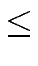 1, 59. 1, 59. |
(45) |
Figure 5:
Complexity of the Karatsuba algorithm.
![\begin{figure}\htmlimage[no_transparent]
\centering
\includegraphics[scale=.5]{kara.ps}\end{figure}](img312.png) |
Subsections


Next: Experimentation
Up: Asymptotically fast algorithms
Previous: Asymptotically fast algorithms
Marc Moreno Maza
2007-01-10
![]()
![]() (n2)
(n2)
![]()
![]() (n)
(n)
![]()
![]()
![]()
![]()