Objectives

Determine the pratical efficiency of the Karatsuba's algorithm in AXIOM or MAPLE. That is, for a pair of ramdom univariate polynomials of degree $n$ determine experimentally which algorithm to use between the Karatsuba's algorithm and the classical (quadratic) one. Obviously, this will depend not only on $n$ but also on the coefficient ring. The following coefficients rings are recommended:

• the ring ${\mathbb{Z}}$ of the integer numbers,
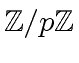• the ring ${\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}$ of the integer modulo 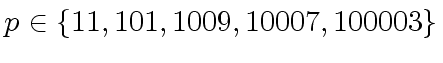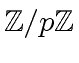$p$ for $p \in \{11, 101, 1009, 10007, 100003\}$ ,
• the ring of univariate polynomials over ${\mathbb{Z}}$ ,
• the ring of univariate polynomials over ${\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}$ for $p \in \{11, 101, 1009, 10007, 100003\}$ .

These choices will become clear later.

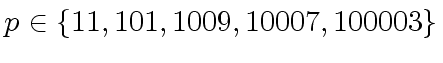If you choose to work with MAPLE, you must implement your own univariate polynomial arithmetic by means of a canonical representation. To do do, you can adapt the file polynomials.input which implements multivariate polynomial arithmetic by means of a canonical representation. This is needed since in your implementation of the Karatsuba's algorithm you must control which algorithm is used during the recursive calls. If you would be using the built-in polynomial multiplication of MAPLE, then you would not know. As you can guess, the MAPLE polynomial multiplication already uses the Karatsuba's algorithm and other tricks.