Project 2 (Rational function reconstruction in AXIOM)
Similar to Project 1, but with an implementation
in AXIOM.
Project 3 (FFT-based multiplication in
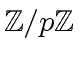
in AXIOM)
The goal of this project is to implement in AXIOM the algorithms of the course
for FFT-based multiplication in
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img13.png) .
Benchmarks versus the Karatsuba and classical quadratic multiplication algorithms
are needed for
.
Benchmarks versus the Karatsuba and classical quadratic multiplication algorithms
are needed for
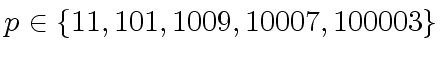 .
.
Project 4 (Fast Interpolation in M
APLE)
We have seen during the course how to perform interpolation
with more than two moduli.
Section 10.2 in [GG99] propose an elegant divide-and-conquer
strategy to improve the performances of the interpolation
Algorithm.
The goal of this project is to implementation this algorithm in MAPLE
and realize benchmarks with
 and
and
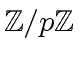 .
.
Project 5 (Fast Chinese Remaindering in M
APLE)
We have seen during the course how to perform Chinese Remaindering
with more than two moduli.
Section 10.3 in [GG99] propose an elegant divide-and-conquer
strategy to improve the performances of the Chinese Remaindering
Algorithm.
The goal of this project is to implementation this algorithm in MAPLE
and realize benchmarks with
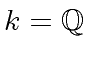 or
or
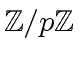 .
.
Project 6 (Fast Interpolation in AXIOM)
Similar to Project 4, but with an implementation
in AXIOM.
Project 7 (Fast Chinese Remaindering in AXIOM)
Similar to Project 5, but with an implementation
in AXIOM.
Project 8 (Project of your choice in M
APLE or AXIOM)
During your reading of [GG99], you may have been seduced or puzzled
by an algorithm.
Please discuss it with the instrutor, to determine if it can
be turned into a project.
Marc Moreno Maza
2008-01-07
 can be reduced
modulo a prime
can be reduced
modulo a prime  ,
provided that
,
provided that 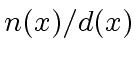 , where
, where
![$ n(x), d(x) \in k[x]$](img7.png) , can be reduced to
, can be reduced to
![$ r \in k[x]$](img8.png) modulo an irreducible polynomial
modulo an irreducible polynomial 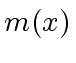 that does not divide
that does not divide
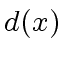 .
The question is how to retrieve
.
The question is how to retrieve
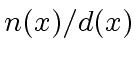 ?
The algorithm is described in Section 5.7 of [GG99].
The goal of this project is to implement this algorithm in MAPLE
and realize benchmarks with
?
The algorithm is described in Section 5.7 of [GG99].
The goal of this project is to implement this algorithm in MAPLE
and realize benchmarks with
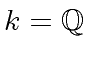 and
and
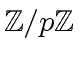 .
.
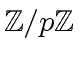 in AXIOM)
The goal of this project is to implement in AXIOM the algorithms of the course
for FFT-based multiplication in
in AXIOM)
The goal of this project is to implement in AXIOM the algorithms of the course
for FFT-based multiplication in
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img13.png) .
Benchmarks versus the Karatsuba and classical quadratic multiplication algorithms
are needed for
.
Benchmarks versus the Karatsuba and classical quadratic multiplication algorithms
are needed for
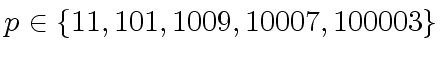 .
.
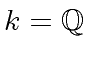 and
and
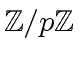 .
.
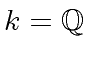 or
or
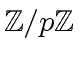 .
.