In the ring
![$ {\mbox{${\mathbb{A}}$}} = {\mbox{${\mathbb{K}}$}}[x]$](img19.png) of univariate polynomials
with coefficients in
of univariate polynomials
with coefficients in
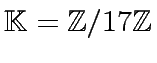 , we consider
the polynomials
, we consider
the polynomials
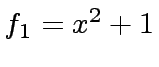 ,
,
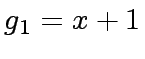 ,
,
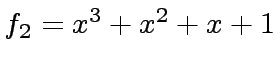 and
and
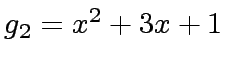 .
Using one of the FFT-based multiplication algorithms described
in the course notes:
.
Using one of the FFT-based multiplication algorithms described
in the course notes:
- compute the product of the polynomials
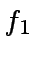 and
and 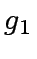
- compute the product of the polynomials
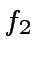 and
and 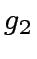
For each product, you should give (at least) the results of each
Discrete Fourier Transforms.
Of course, you should better choose primitive roots of unity that minize
the number of required operations in
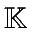 .
.
Answer 3

Answer 4

Answer 5

Answer 6

Marc Moreno Maza
2008-01-31
![$ {\mbox{${\mathbb{A}}$}} = {\mbox{${\mathbb{K}}$}}[x]$](img19.png) of univariate polynomials
with coefficients in
of univariate polynomials
with coefficients in
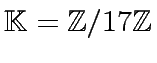 , we consider
the polynomials
, we consider
the polynomials
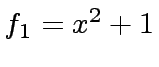 ,
,
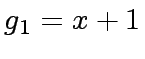 ,
,
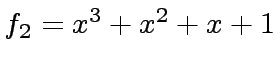 and
and
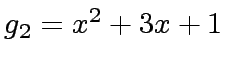 .
Using one of the FFT-based multiplication algorithms described
in the course notes:
.
Using one of the FFT-based multiplication algorithms described
in the course notes: