Next: About this document ... Up: Quiz4 Previous: Exercise 2.
![$ m \in {\mbox{${\mathbb{Q}}$}}[x]$](img57.png) be a non-constant polynomial of degree
be a non-constant polynomial of degree ![$ R = Q[x] / \langle m \rangle$](img58.png) be the set of the residue
classes modulo
be the set of the residue
classes modulo ![$ p \in {\mbox{${\mathbb{Q}}$}}[x]$](img59.png) be a polynomial. How many elements are there
in the residue class
be a polynomial. How many elements are there
in the residue class
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img47.png) we want to decide whether there exists
a polynomial
we want to decide whether there exists
a polynomial 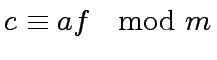 .
For instance, with
.
For instance, with
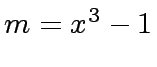 ,
, 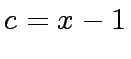 and
and
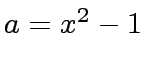 ,
one solution is
,
one solution is
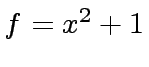 .
Indeed, we have
.
Indeed, we have
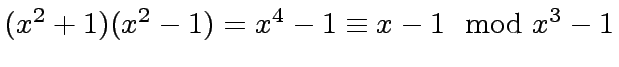 .
(Working modulo
.
(Working modulo  means replacing every occurrence of
means replacing every occurrence of 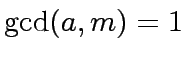 . Explain why such a polynomial
. Explain why such a polynomial 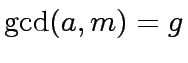 where
where 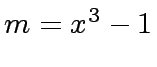 ,
,
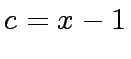 and
and
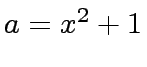 .
.
![\fbox{
\begin{minipage}{13 cm}
\begin{enumerate}
\item[1.] Only one! The remaind...
...\mod{m}.$
Hence $f = x^2 - 1$\ is the solution!
\end{enumerate} \end{minipage}}](img76.png)
Marc Moreno Maza