Next: About this document ... Up: Quiz5 Previous: Exercise 1.
![$ {\mbox{${\mathbb{A}}$}} = {\mbox{${\mathbb{K}}$}}[x]$](img19.png) of univariate polynomials
with coefficients in
of univariate polynomials
with coefficients in
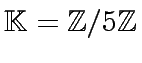 , we consider
the polynomials
, we consider
the polynomials
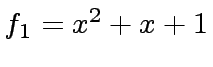 ,
,
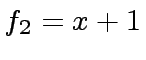 ,
,
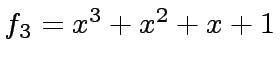 .
.
For every pair
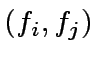 , with
, with
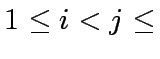 such that we can compute the product
such that we can compute the product 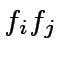 by means of the FFT-based algorithm studied in class:
by means of the FFT-based algorithm studied in class:
Marc Moreno Maza