Next: Exercise 1. Up: Quiz8 Previous: Formula: Fermat's little Theorem
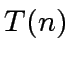 be the running time estimate of a divide-and-conquer algorithm.
Assume that
be the running time estimate of a divide-and-conquer algorithm.
Assume that 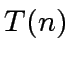 satisfies a relation of the form:
satisfies a relation of the form:
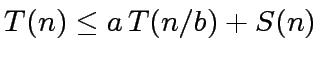 |
(5) |
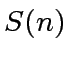 is the cost of the combine-part,
is the cost of the combine-part, 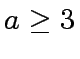 is the
number of recursive calls and
is the
number of recursive calls and 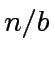 is the size of a sub-problem, with
is the size of a sub-problem, with 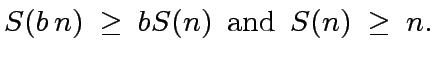 |
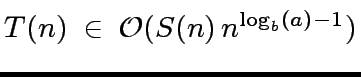 .
.
Marc Moreno Maza