Next: About this document ... Up: Quiz8 Previous: Exercise 2.
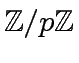 for
for 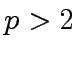 .
(In fact, what follows would work with any coefficient
ring
.
(In fact, what follows would work with any coefficient
ring
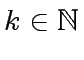 , be the smallest power of
, be the smallest power of 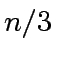 .
(For simplicity, you can assume that
.
(For simplicity, you can assume that 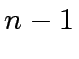 and that
and that 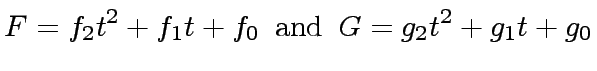 |
(7) |
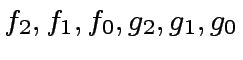 are polynomials
of degree less than
are polynomials
of degree less than 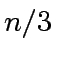 .
Let
.
Let 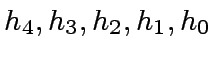 of degree less than
of degree less than 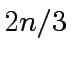 such that we have
such that we have
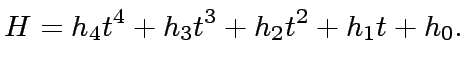 |
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img66.png) . We denote these polynomials
by
. We denote these polynomials
by 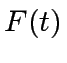 ,
, 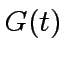 ,
, 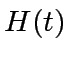 ;
they have respective degrees
;
they have respective degrees 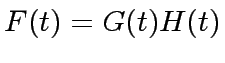 .
We evaluate
.
We evaluate 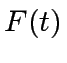 and
and 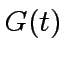 at
at 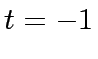 and
and 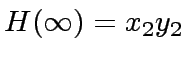 .
Hence we have
.
Hence we have
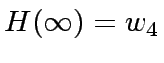 .
.
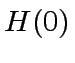 ,
, 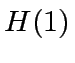 ,
, 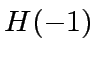 ,
, 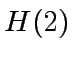 and
and
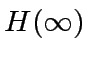 requires:
requires:
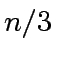 ,
,
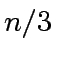 ,
,
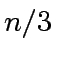 by a power of
by a power of 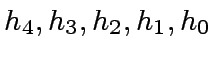 can be computed from
can be computed from 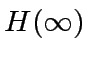 ,
, 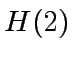 ,
, 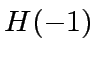 ,
, 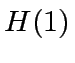 ,
, 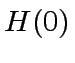 ,
by solving the following system of linear equations:
,
by solving the following system of linear equations:
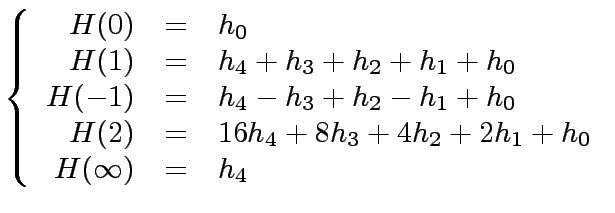 |
(8) |
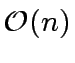 operations in
operations in
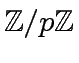 .
.
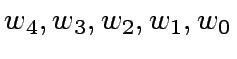 of
of 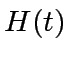 .
This provides, in fact, an algorithm for multiplying
univariate polynomials in
.
This provides, in fact, an algorithm for multiplying
univariate polynomials in
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img66.png) .
Let us estimate its time complexity.
Let
.
Let us estimate its time complexity.
Let 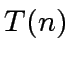 be the number of operations in
be the number of operations in
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img66.png) that are needed for computing
that are needed for computing 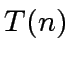 satisfies a relation of the form
satisfies a relation of the form
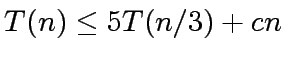 |
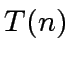 and compare with the time complexity of Karatsuba's multiplication.
and compare with the time complexity of Karatsuba's multiplication.
Marc Moreno Maza