

Next: Exercise 2
Up: The Assignment
Previous: The Assignment
We consider the grammar G with
- the four terminals ( , ) , , and
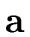 (the opening parenthesis, the closing parenthesis, the comma and the lower-case
letter a)
(the opening parenthesis, the closing parenthesis, the comma and the lower-case
letter a)
- the three non-terminals S, L, E
- the start symbol S
- the six productions below
| S |
 |
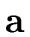 |
| S |
 |
L |
| L |
 |
() |
| L |
 |
(E) |
| E |
 |
S |
| E |
 |
E , S |
Let 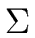 be the alphabet consisting
of the four terminals of G. Hence
be the alphabet consisting
of the four terminals of G. Hence
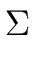 = {(, ), ,, = {(, ), ,, 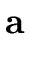 } } |
(1) |
Let L be the language over 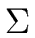 generated by G.
generated by G.
- Is the language L regular?
- Show that the language L is context-free.
- We consider the following five words over
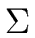
| w1 |
= |
(a, a) |
| w2 |
= |
(a, (a, a)) |
| w3 |
= |
(a), (a, a) |
| w2 |
= |
(a, ((a, a), (a, a))) |
| w4 |
= |
((a, a, a), (a)) |
Which of these words belong to L?
For those words which belong to L, give
a leftmost derivation and a rightmost derivation.
- Is the grammar G left recursive?
If yes, construct a grammar G' which is not left recursive
and which generates L.
If not we define G' = G.
- Is the grammar G' LL(1)?


Next: Exercise 2
Up: The Assignment
Previous: The Assignment
Marc Moreno Maza
2004-12-01