

Next: A starting point for the
Up: Compiler Theory: Assignment 3
Previous: The factorial
WRITING TRANSLATION SCHEMES WITH YACC.
In all our previous examples with YACC we were
- evaluating synthesized attributes
- by putting actions at the end of each production rule.
This works because a YACC parser is a bottom-up parser.
But in fact YACC can do more.
- A YACC program (where productions are embedded with actions)
is a translation scheme.
- Thus, a YACC parser evaluates the actions by a depth-first traversal
of the parse tree.
HOW YACC HANDLES PRODUCTIONS EMBEDDED WITH ACTIONS? An action occurring inside the right side of a production
- can be replaced by a new dummy non-terminal
- that generates the empty string
- and produces the corresponding action.
For instance the following translation scheme fragment
| A |
 |
B1 {e1} B2 {e2} B3 {e3} |
is equivalent to
| A |
 |
B1 C1 B2 C2 B3 C3 |
| C1 |
 |
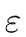 {e1} {e1} |
| C2 |
 |
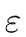 {e2} {e2} |
| C3 |
 |
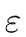 {e3} {e3} |
In YACC
- the parser implemented in YACC requires that the actions occur at the end of the right side
of the productions.
- Then, for actions occurring inside the right side, YACC automatically generates marker non-terminals generating the empty word. Hence
thing: A { printf("seen on A"); } B ;
is automatically transformed into something like
thing: A fakename B ;
fakename: /* empty */ {printf("seen on A"); } ;
- Therefore, YACC interprets an embedded action as a symbol in the rule.
So one can have:
thing: A { $$ = 17; } B C { printf("%d",$2); }
where $1, $2, $3, $4 refers respectively to A,
{ ... }, B, C.
PASSING IDENTIFIER TYPES Consider the following translation scheme.
| D |
 |
T {L.in :=
T.type} L |
| T |
 |
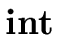 {T.type := {T.type :=
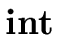 } } |
| T |
 |
 {T.type := {T.type :=
 } } |
| L |
 |
{ L1.in := L.in }
L1 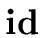 |
| |
|
{ addtype
(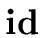 .entry, L.in) } .entry, L.in) } |
| L |
 |
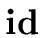 { addtype
( { addtype
(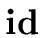 .entry, L.in) } .entry, L.in) } |
Consider the following sentence generated by the above grammar.
real p, q, r
A bottom-up parse of this sentence will result in applying backwards the rules
below in this order:
-
T


-
L

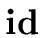
-
L
 L,
L,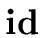
-
L
 L,
L,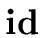
-
D
 TL
TL
When
- considering
L

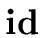 or
L
or
L  L,
L,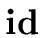
- together with the action addtype
(
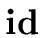 .entry, L.in)
.entry, L.in)
one needs the inherited attribute L.in.
Observe that
- L.in was computed just before considering
L

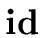 or
L
or
L  L,
L,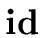 .
.
- So it will be the immediate previous attribute computed by a depth-first traversal.
- YACC refers to it as $-1
- $n with
n = - 2, - 3... can be used also.
- If a production is embedded with more than one actions
a1, a2,..., an
and if an action ai with i < n defines $$ then aj with j > i
can refer to it as $0.
PASSING INHERITED ATTRIBUTES. In a situation like
| S |
 |
aA {C.i :=
A.s} C |
| S |
 |
bAB {C.i :=
A.s} C |
| C |
 |
c {C.s := g(C.i)} |
In a YACC program for this translation scheme how to access to C.i
- in the third rule
- if we do not know which rule was applied before?
The solution is to use a dummy nonterminal, called a marker.
We change the above translation scheme to
| S |
 |
aA {C.i :=
A.s} C |
| S |
 |
bAB {M.i :=
A.s} M {C.i :=
M.s} C |
| M |
 |
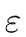 {M.s := M.i} {M.s := M.i} |
| C |
 |
c {C.s := g(C.i)} |
Then a YACC program for the above translation scheme will look like:
S : a A C
| b A B M C
;
M : /* empty */ {$$ = $-2}
;
C : c {$$ = g($-1)} ;


Next: A starting point for the
Up: Compiler Theory: Assignment 3
Previous: The factorial
Marc Moreno Maza
2004-12-01