


Next: Global Live Variable Analysis
Up: Compiler Theory: Code Optimization
Previous: Data-flow analysis: copy propagation.
IN PERFORMING COMMON SUBEXPRESSION ELIMINATION we wish tofind in the program two expressions that will always yield the same value,
such that one can be replaced by the other.
AN EXPRESSION B OP C IS AVAILABLE at a point p of the program if
- all routes (= pathes) from the start of the program to that point p
must pass through the evaluation of b op c, and
- after the (last) evaluation of b op c there are no redefinitions
of b or c.
This means that at point p we can replace b op c
by the result of its last evaluation.
DATA-FLOW EQUATIONS.
- The expression b op c is generated by a statement where this expression is evaluated.
Similarly, the expression b op c is killed by a statement that redefines b or c.
- Therefore, we can again think of killing and generating available expressions.
- The set genE(B) of the expressions generated by a basic block B can be computed
(or defined) as follows.
- Initially, we set
genE(B) =
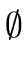 .
.
- Going through the statements of B in sequence,
- for a statement a := b op c add b op c to genE(B) and
- remove from genE(B) any expression containing a.
- Let E be the set of all the expressions in the entire program
 .
The set killE(B) of the expressions killed by a basic block B can be computed
(or defined) as follows.
.
The set killE(B) of the expressions killed by a basic block B can be computed
(or defined) as follows.
- Initially, we set
killE(B) =
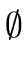 .
.
- Going through the statements of B in sequence,
for a statement a := b op c add to killE(B) any expression in E containing a.
- Precautionary principles:
- we only add an expression to genE(B) if we are sure that it will be evaluated
- if there is a possibility that the expression is killed, we add it to killE(B).
- For a basic block B we define
- inE(B) as the set of the expressions available at entry(B),
- outE(B) as the set of the expressions available at exit(B).
DATA-FLOW EQUATIONS. For every basic block B the data-flow sets inE(B) and outE(B) satisfy
the following equations
| inE(B) |
= |
 outE(B'), outE(B'), |
| outE(B) |
= |
genE(B)   inE(B) inE(B)  killE(B) killE(B) . . |
|
(10) |
COMPUTING THE DATA-FLOW SETS. We assume that
- the set E of all expressions in the entire program
 has been computed,
has been computed,
- the data-flow sets killE(B) and genE(B) have been computed
for every basic block B.
The iterative algorithm for determining available expressions is
now basically the same as for copy statements.
- For the first basic block B1 we define
inE(B1) =  and outE(B1) = genE(B1). and outE(B1) = genE(B1). |
(11) |
- For each basic block
B
 B1 we define
B1 we define
outE(B) = E  killE(B) killE(B) |
(12) |
- We update the data-flow sets inE(B) and outE(B) (for every basic block
B
 B1) with the data-flow equations until there are no more changes
in these sets.
B1) with the data-flow equations until there are no more changes
in these sets.



Next: Global Live Variable Analysis
Up: Compiler Theory: Code Optimization
Previous: Data-flow analysis: copy propagation.
Marc Moreno Maza
2004-12-02
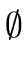 .
.
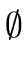 .
.
 outE(B'),
outE(B'),