

Next: Exercise 4.
Up: Final-2003
Previous: Exercise 2.
We consider the alphabet
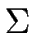 = {a, b}
and the grammar G below.
Let L be the language generated by G over
= {a, b}
and the grammar G below.
Let L be the language generated by G over 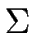 .
.
| G |
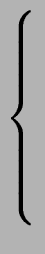 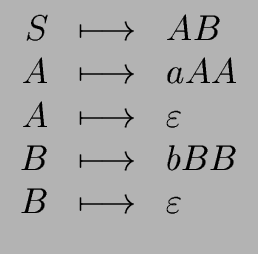 |
|
|
- Give a grammar G' generating
L
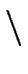 {
{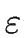 } and
with no
} and
with no
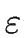 -productions, that is
no rules of the form
X
-productions, that is
no rules of the form
X 
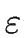 ,
where
,
where
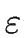 denotes the empty word.
denotes the empty word.
- If L is regular then
give a regular expression for L
otherwise tell whether G' is anbiguous or not.
Answer 3



Next: Exercise 4.
Up: Final-2003
Previous: Exercise 2.
Marc Moreno Maza
2004-12-02