

Next: Exercise 8.
Up: Final-2003
Previous: Exercise 6.
We consider the following grammar.
As in the course,
the nonterminals P, D, S, T, E stand for
Program, Declaration, Statement, Type, Expression.
The terminals id, boolean, integer, literal, num
stand for identifier, boolean (as a type), integer (as a type),
boolean literal (as a value), integer number (as a value).
P  D; S D; S |
D  D; D D; D |
D  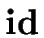 : T : T |
T  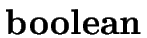 |
T   |
E  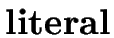 |
E  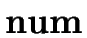 |
E  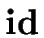 |
E  E E 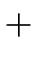 E E |
E  E E 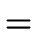 E E |
S  S1; S2 S1; S2 |
S  E E |
S  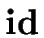 := S1 := S1 |
S  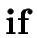 E E 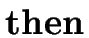 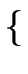 S1 S1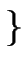 |
S  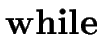 E E 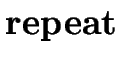 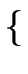 S1 S1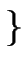 |
There's one sligth difference w.r.t. the grammar
of the course in the Type checking chapter:
each valid statement has a value and thus a type
(rather than no value and type void).
The following rules compute the value
of a valid statement.
- if S1 and S2 are valid statements
then the value of
S1; S2 is that of S2.
- if
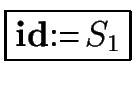 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
- if
 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
- if
 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
We associate attributes T.type, E.type, S.type,
to the grammar symbols T, E, S.
Each of these attributes may be boolean, integer or type_error.
Then, for instance, the statement
 is valid as soon as
E.type =
is valid as soon as
E.type = 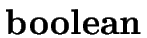 and
S1.type
and
S1.type 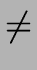
 .
The attribute
.
The attribute
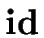 .entry refers to the entry of
.entry refers to the entry of 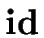 in the symbol table.
in the symbol table.
Question. Complete the following type checker for the above grammar.


Next: Exercise 8.
Up: Final-2003
Previous: Exercise 6.
Marc Moreno Maza
2004-12-02


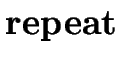
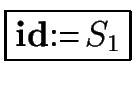 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
 is valid as soon as
E.type =
is valid as soon as
E.type =  .
The attribute
.
The attribute