

Next: Exercise 2.
Up: Quiz10
Previous: Guidelines.
We consider the alphabet
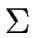 = {
= {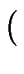 ,
,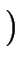 }
consisting of the opening parenthesis and the closing parenthesis.
For each of the following grammars, if its generated language
is regular, then give a finite automaton recognizing this language,
otherwise justify briefly why it is not regular.
}
consisting of the opening parenthesis and the closing parenthesis.
For each of the following grammars, if its generated language
is regular, then give a finite automaton recognizing this language,
otherwise justify briefly why it is not regular.
Answer 1



Next: Exercise 2.
Up: Quiz10
Previous: Guidelines.
Marc Moreno Maza
2004-12-02