

Next: About this document ...
Up: Quiz10
Previous: Exercise 3.
Recall that for any string 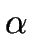 of symbols the set FIRST(
of symbols the set FIRST(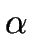 )
satisfies the following conditions for every terminal a and every string of symbols
)
satisfies the following conditions for every terminal a and every string of symbols 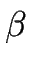
- FIRST(
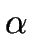 )
)
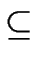 VT
VT 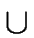 {
{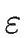 }
}
-
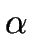
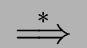 a
a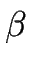 iff a
iff a 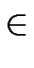 FIRST(
FIRST(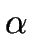 )
)
-
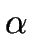

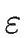 iff
iff
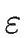
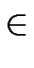 FIRST(
FIRST(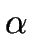 ).
).
For a symbol
X 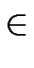 VT
VT 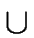 VN the set FIRST(X) can be computed as follows
VN the set FIRST(X) can be computed as follows
Algorithm 1
![\fbox{
\begin{minipage}{13 cm}
\begin{description}
\item[{\bf Input:}] $X \in V_...
...) := {\sc FIRST}($X$) ${\cup} \ \{ {\varepsilon} \}$\end{tabbing}\end{minipage}}](img31.png)
Algorithm 2
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $X = X_1 ...
...) := {\sc FIRST}($X$) ${\cup} \ \{ {\varepsilon} \}$\end{tabbing}\end{minipage}}](img32.png)
Recall that FOLLOW(A) is the set of the terminals that can appear
immediately to the right of the nonterminal A in some sentential form.
Moreover $ belongs to FOLLOW(A) if A is the rightmost
symbol in some sentential form.
Algorithm 3
![\fbox{
\begin{minipage}{13 cm}
\begin{description}
\item[{\bf Input:}] $G = (V_T...
...} \\
\> \> \> \> \> \> \> $M[A,a]$\ := {\em error}
\end{tabbing}\end{minipage}}](img33.png)


Next: About this document ...
Up: Quiz10
Previous: Exercise 3.
Marc Moreno Maza
2004-12-02