

Next: Exercise 4.
Up: Quiz5
Previous: Exercise 2.
Let 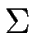 be the alphabet consisting of the opening parenthesis, the closing parenthesis, the comma and the lower-case letter a.
That is
be the alphabet consisting of the opening parenthesis, the closing parenthesis, the comma and the lower-case letter a.
That is
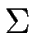 = {(, ), ,,
= {(, ), ,, 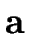 }.
Let G be the grammar over
}.
Let G be the grammar over 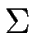 , with non-terminals S, L, E,
start symbol S and the six productions below
, with non-terminals S, L, E,
start symbol S and the six productions below
| S |
 |
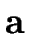 |
| S |
 |
L |
| L |
 |
() |
| L |
 |
(E) |
| E |
 |
S |
| E |
 |
E , S |
Let 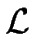 be the language over
be the language over 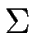 generated by G.
For each of the words below, if it belongs to
generated by G.
For each of the words below, if it belongs to 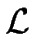 , then give
a derivation from S to this word.
, then give
a derivation from S to this word.
| w1 |
= |
(a, a) |
w2 |
= |
(a, (a, a)) |
| w3 |
= |
(a), (a, a) |
w4 |
= |
((a, a, a), (a)) |
Answer 3



Next: Exercise 4.
Up: Quiz5
Previous: Exercise 2.
Marc Moreno Maza
2004-12-02