


Next: About this document ...
Up: Quiz2
Previous: Exercise 2.
Let a and b be two univariate polynomials in
 [x].
We assume that b is monic and has degree n > 0
and that a has degree n + k whith k
[x].
We assume that b is monic and has degree n > 0
and that a has degree n + k whith k 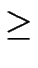 0.
We define
a = an+kxn+k + ... + anxn + ... + a1x + a0 and
b = bnxn + ... + b1x + b0.
We are interesting in computing the remainder r
of the Euclidean division of a by b (regarding them
as polynomials in
0.
We define
a = an+kxn+k + ... + anxn + ... + a1x + a0 and
b = bnxn + ... + b1x + b0.
We are interesting in computing the remainder r
of the Euclidean division of a by b (regarding them
as polynomials in
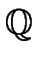 [x]), by a modular method.
Let p be a prime number and
[x]), by a modular method.
Let p be a prime number and  be the application that
maps every integer z with its residue class
be the application that
maps every integer z with its residue class
 (z) in
(z) in
 /p
/p .
We extend this application to a map denoted
.
We extend this application to a map denoted  again,
from
again,
from
 [x] to
[x] to
 /p
/p [x], such that x is mapped to x.
[x], such that x is mapped to x.
- Explain why the remainder r belongs to
 [x], that is
no fractions appears during the computations.
[x], that is
no fractions appears during the computations.
- Consider
a = x2 + 7x + 1 and b = x + 4. Compute q and r.
- Consider p = 3. Compute
 (a) and
(a) and
 (b).
Then compute the quotient and the remainder of
(b).
Then compute the quotient and the remainder of
 (a) by
(a) by
 (b).
(b).
- In the general case, what is the relation between r and the remainder
of
 (a) by
(a) by
 (b)?
(b)?
- Design a modular method to compute r.
Answer 4

Answer 5




Next: About this document ...
Up: Quiz2
Previous: Exercise 2.
Marc Moreno Maza
2006-01-09
 (a) and
(a) and
 (b).
Then compute the quotient and the remainder of
(b).
Then compute the quotient and the remainder of
 (a) by
(a) by
 (b).
(b).
 (a) by
(a) by
 (b)?
(b)?
 be the application that
maps every integer z with its residue class
be the application that
maps every integer z with its residue class
 (z) in
(z) in
 again,
from
again,
from
 (a) and
(a) and
 (b).
Then compute the quotient and the remainder of
(b).
Then compute the quotient and the remainder of
 (a) by
(a) by
 (b).
(b).
 (a) by
(a) by
 (b)?
(b)?