

Next: Modular inverses using Newton iteration
Up: Division with remainder using Newton
Previous: Classical division with remainder
We shall see now that the complexity result
of Proposition 5
can be improved.
To do so, we will show that q can be computed from a and b
by performing essentially one multiplication in R[x].
We start with the equation
| a(x) = q(x) b(x) + r(x) |
(65) |
where a, b, q and r are in the statement of
Proposition 5.
Replacing x by 1/x and multiplying the equation by xn
leads to the new equation:
xn a(1/x) =  xn-mq(1/x) xn-mq(1/x)  xm b(1/x) xm b(1/x)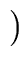 + xn-m+1 + xn-m+1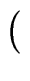 xm-1 r(1/x) xm-1 r(1/x)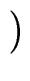 |
(66) |
In Equation (66)
each of the rational fractions a(1/x), b(1/x), q(1/x) and r(1/x)
is multiplied by xe such that e is an upper bound for the degree of its denominator.
So Equation (66) is in fact
an equation in R[x].
Definition 5 and
Proposition 6
highlight this fact.
Then
Proposition 7
and
Theorem 9
suggest Algorithm 6
which provides an efficient way to compute the inverse
of a univariate polynomial in x modulo a power of x.
Finally we obtain
Algorithm 7
for fast division with remainder based on
Equation (66).
Definition 5
For a univariate polynomial
p =
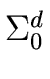 pixi
pixi in
R[
x]
with degree
d and an integer
k 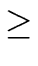 d
d, the
reversal of order k
of
p is the polynomial denoted by
revk(
p) and defined by
revk(p) = xk p(1/x) = 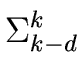 pk-ixi. pk-ixi. |
(67) |
When
k =
d the polynomial
revk(
p) is simply denoted by
rev(
p).
Hence we have
| rev(p) = pd + pd-1x + ... + p1xd-1 + p0xd. |
(68) |
Proposition 6
With
a,
b,
q and
r as abovce, we have
revn(a) 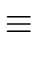 revn-m(q) revm(b) modxn-m+1 revn-m(q) revm(b) modxn-m+1 |
(69) |
Proof.
Indeed with Definition
5
Equation (
66)
reads
| revn(a) = revn-m(q) revm(b) + xn-m+1 revm-1(r) |
(70) |
leading to the desised result.

Remark 11
If R is a field then we know that
revn-m(q) is invertible
modulo xn-m+1.
Indeed,
revn-m(q) has constant coefficient 1 and thus the
gcd of
revn-m(q) and xn-m+1 is 1.
The case where R is not a field leads also to a simple
and surprising solution as we shall see in the next section.


Next: Modular inverses using Newton iteration
Up: Division with remainder using Newton
Previous: Classical division with remainder
Marc Moreno Maza
2004-04-27
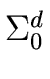 pixi in R[x]
with degree d and an integer k
pixi in R[x]
with degree d and an integer k 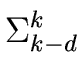 pk-ixi.
pk-ixi.