

Next: Quadratic Hensel Lifting
Up: Hensel Lifting
Previous: Hensel Lifting
Theorem 15
Let
R be a commutative ring with identity element.
Let
f,
g0,
h0 be univariate polynomials in
R[
x]
and let
m  R
R.
We assume that the following relation holds
f 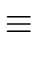 g0 h0 modm g0 h0 modm |
(121) |
We assume also that
g0 and
h0 are relatively prime modulo
m,
that is there exists
s,
t  R
R such that
sg0 + th0 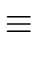 1 modm 1 modm |
(122) |
Then, for every integer
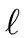
there exist
g( )
),
h( )
)  R
R[
x] such that we have
-
f
 g(
g( )h(
)h( )modm
)modm ,
,
-
g0
 g(
g( )modm.
)modm.
Proof.
We apply Theorem
13 with
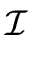 = = 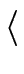 m m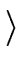 , n = 1, r = 2, f1(x1, x2) = x1x2 - f. , n = 1, r = 2, f1(x1, x2) = x1x2 - f. |
(123) |
Thus we have
U = 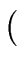 u11 u12 u11 u12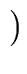 = =  g0 h0 g0 h0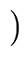 |
(124) |
Observe that this matrix is left-invertible modulo
m if and only if
g0,
h0
are relatively prime modulo
m.
Indeed, the matrix
U is left-invertible modulo
m iff there exists
a matrix
such that
U U-1 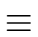
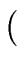
1
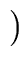
mod
m, that is
sg0 + th0 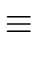 1 modm 1 modm |
(125) |
We prove now the claim of the theorem.
Assume we have computed
g( )
),
h( )
)  R
R
such that
f 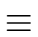 g(
g( )h(
)h( )
)mod
m
and
g 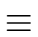 g(
g( )
)mod
m hold.
We want to compute
g( +1)
+1),
h( +1)
+1)  R
R.
Let
v be such that
f1(g( ), h( ), h( )) = g( )) = g( )h( )h( ) - f = vm ) - f = vm |
(126) |
We look for
g
,
h
 R
R such that
g( +1) = g( +1) = g( ) + g ) + g m m and h( and h( +1) = h( +1) = h( ) + h ) + h m m |
(127) |
Following the proof of Theorem
13 we are led to solve the equation
v + g h0 + h h0 + h g0 g0 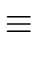 0 modm 0 modm |
(128) |
A solution of this equation is
This proves the claim of the theorem.

Remark 23
The proof of Theorem 15 provides
a solution
(g , h
, h ) to
Equation (128).
It is desirable to add constraints such that
Equation (128)
has a unique soulution.
In particular, one would like to guarantee that for every integer
) to
Equation (128).
It is desirable to add constraints such that
Equation (128)
has a unique soulution.
In particular, one would like to guarantee that for every integer 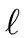 the polynomials
g(
the polynomials
g( ) and g0 have the same degree.
This problem is solved in the following sub-section
where we study Linear Diophantine Equations.
) and g0 have the same degree.
This problem is solved in the following sub-section
where we study Linear Diophantine Equations.
Definition 10
Let
R be a commutative ring with identity element.
A
linear Diophantine equation over
R is an equation
of the form
| f1s1 + ... + fnsn = a |
(130) |
where
f1,...,
fn,
a are given in
R
and where
s1,...,
sn are unknowns in
R.
Theorem 16
Let
R be an Euclidean domain and let
f,
g,
h,
a  R
R
such that
h = gcd(
f,
g).
We consider the linear Diophantine equation
Then the following hold
- (i)
- Equation (131) has a solution
if and only if h divides a.
- (ii)
- If h
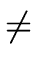 0 and if
(s0, t0)
0 and if
(s0, t0)  R2 is a solution of
Equation (131)
then every other solution is of the form
R2 is a solution of
Equation (131)
then every other solution is of the form
(s0 + r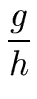 , t0 - r , t0 - r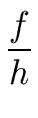 ) where r ) where r 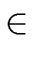 R. R. |
(132) |
- (iii)
- If R = F[x] where F is a field, h
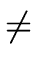 0, and if
Equation (131)
is solvable, where
0, and if
Equation (131)
is solvable, where
| degf + degg - degh > dega |
(133) |
then there is a unique solution
(s0, t0)  R2 of
Equation (131)
such that
R2 of
Equation (131)
such that
| degs < degg - degh and degt < degf - degh. |
(134) |
Proof.
First we prove (
i).
If
(
s0,
t0)
 R2
R2 is a solution of Equation (
131),
then
h which divides
s0f +
t0g, divides also
a.
Conversly, we assume that
h = gcd(
f,
g) divides
a.
The claim is trivial if
h = 0. (Indeed, this implies
f =
g = 0 and also
a = 0.)
Otherwise, let
(
s0,
t0)
 R2
R2 be computed by the Extended Euclidean Algorithm
applied to (
f,
g), such that we have
s0f +
t0g =
h.
Then
(
s,
t) = (
s0a/
h,
t0a/
h) is a solution of
Equation (
131).
Now we prove (ii). Assume h 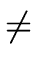 0 and let
(s0, t0)
0 and let
(s0, t0)  R2 is a solution of
Equation (131).
Since h
R2 is a solution of
Equation (131).
Since h 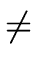 0, then f /h and g/h are coprime.
Let (s, t) be in R2.
Then we have
0, then f /h and g/h are coprime.
Let (s, t) be in R2.
Then we have
| sf + tg = a |
 |
(s - s0)f + (t - t0)g = 0 |
| |
 |
(s - s0)(f /h) = - (t - t0)(g/h) |
| |
 |
(s - s0)(f /h) = (t0 - t)(g/h) |
| |
 |
(g/h) | (s - s0) and (f /h) | (t0 - t) |
| |
 |
(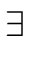 r r 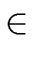 R) (s - s0) = r(g/h) and (t0 - t) = r(f /h) R) (s - s0) = r(g/h) and (t0 - t) = r(f /h) |
| |
 |
(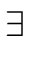 r r 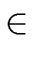 R) s = s0 + r(g/h) and t = t0 - r(f /h). R) s = s0 + r(g/h) and t = t0 - r(f /h). |
|
|
Finally, we prove (
iii). Let
(
s1,
t1)
 R2
R2 be a solution of
Equation (
131).
Let
q and
t0 be the quotient and the remainder of
t1 w.r.t.
f /
h.
Hence we have
| t1 = f /hq + t0 and degt0 < degf - degh. |
(135) |
We define
Observe that
| (s0, t0) = (s1, t1) + q(g/h, - f /h) |
|
solves Equation (
131) too.
By Relation (
135) and by hypothesis we have
| deg(t0g) < degf + degg - degh and dega < degf + degg - degh |
|
leading to
| degs0 + degf = degs0f = deg(a - t0g) < degf + degg - degh. |
|
Therefore we have
| degt0 < degf - degh and degs0 < degg - degh. |
|
This proves the existence. Let us prove the unicity.
Let (
s,
t) be a solution of Equation (
131).
We know that there exists
r  R
R such that
s =
s0 +
rg/
h.
Since
deg
s0 < deg
g - deg
h holds, if
r 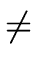
0, we have
degs 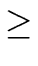 deg(g/h) = degg - degh. deg(g/h) = degg - degh. |
|
This implies the uniquemess.

Theorem 17
Let
R be a commutative ring with identity element.
Let
f,
g0,
h0 be univariate
monic polynomials in
R[
x].
Let
m  R
R be such that
R/
m is a field.
We assume that the following relation holds
f 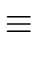 g0 h0 modm g0 h0 modm |
(137) |
and that
g0 and
h0 are relatively prime modulo
m.
Then, for every integer
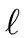
there exist
unique monic polynomials
g( )
),
h( )
)  R
R[
x] such that we have
-
f
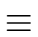 g(
g( )h(
)h( )modm
)modm ,
,
-
g0
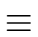 g(
g( )modm,
)modm,
-
h0
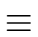 h(
h( )modm.
)modm.
Proof.
By induction on
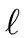
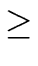
1.
The clain is clear for
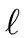
= 1.
So let us assume it is true for
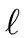
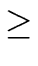
1
and consider monic polynomials
g( +1)
+1),
h( +1)
+1)  R
R[
x]
satisfying
and
g0  g( g( +1)modm and h0 +1)modm and h0  h( h( +1)modm. +1)modm. |
(139) |
Such polynomials
g( +1)
+1),
h( +1)
+1) exist
by Theorem
15.
(The fact that they can be chosen monic is left to the reader
as an exercise.)
Observe that we have
So the induction hypothesis leads to
g( ) )  g( g( +1)modm +1)modm and h( and h( ) )  h( h( +1)modm +1)modm |
(141) |
Hence there exist polynomials
qg,
qh 
(
R/
m)[
x] such that
g( +1) = g( +1) = g( ) + m ) + m qg and h( qg and h( +1) = h( +1) = h( ) + m ) + m qh. qh. |
(142) |
Since
f,
g0,
h0 are given to be monic, it is easy to prove
that for
k 
1 we have
| degqg < degg0 and degqh < degh0 |
(143) |
In addition, observe that combining
Equation (
138)
and
Equation (
142)
we obtain
| f |
 |
g( )h( )h( ) + ) +  g( g( )qh + h( )qh + h( )qg )qg m m modm modm +1 +1 |
|
(144) |
The induction hypothesis shows that
f -
g( )h(
)h( )
) is a multiple of
m
.
Then we obtain
g0qh + h0qg   modm. modm. |
(145) |
By Theorem
16
and
Equation (
143),
the Equation (
145)
has a unique solution.



Next: Quadratic Hensel Lifting
Up: Hensel Lifting
Previous: Hensel Lifting
Marc Moreno Maza
2004-04-27
 g(
g( )h(
)h( )modm
)modm ,
,
 g(
g( )modm.
)modm.
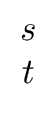
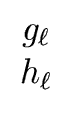

![]() 0 and let
(s0, t0)
0 and let
(s0, t0) ![]() R2 is a solution of
Equation (131).
Since h
R2 is a solution of
Equation (131).
Since h ![]() 0, then f /h and g/h are coprime.
Let (s, t) be in R2.
Then we have
0, then f /h and g/h are coprime.
Let (s, t) be in R2.
Then we have