Let n be a positive integer and
![]()
![]() R be a primitive n-th
root of unity.
In what follows we identify every univariate polynomial
R be a primitive n-th
root of unity.
In what follows we identify every univariate polynomial
f =  fi xi fi xi |
(13) |
DFT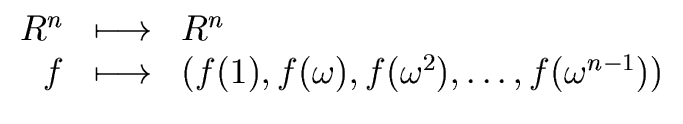 |
(14) |
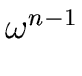 )
is the matrix of the R-linear map
DFT
)
is the matrix of the R-linear map
DFT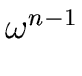 )
is invertible which holds iff the values
1,
)
is invertible which holds iff the values
1,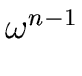 are pairwise different.
A relation
are pairwise different.
A relation
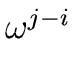 ) = 0.
Since
(1 -
) = 0.
Since
(1 - 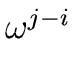 ) cannot be zero or a zero divisor
then
) cannot be zero or a zero divisor
then
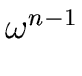 are pairwise different and
DFT
are pairwise different and
DFT
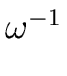 the inverse of
the inverse of V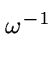 = nIn = nIn |
(15) |
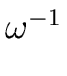 .
Observe that
.
Observe that
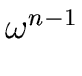 .
Thus
.
Thus
Let us consider the product of the matrix
V![]() and
V
and
V![]()
![]() .
The element at row i and column k is
.
The element at row i and column k is
|
(16) |
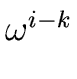 is either a power of
is either a power of