Convolution of polynomials

Let n be a positive integer and $\omega$ $\in$ R be a primitive n-th root of unity.

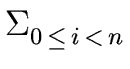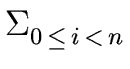Definition 3 The convolution w.r.t. n of the polynomials f = $\Sigma_{{{0 \, \leq \, i \, < \, n}}}^{{}}$ f_i xⁱ and g = $\Sigma_{{{0 \, \leq \, i \, < \, n}}}^{{}}$ g_i xⁱ in R[x] is the polynomial

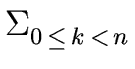h = $\displaystyle \Sigma_{{{0 \, \leq \, k \, < \, n}}}^{{}}$ h_k x^k

(17)

such that for every k = 0^...n - 1 the coefficient h_k is given by

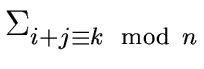h_k = $\displaystyle \Sigma_{{{i+j \equiv k \mod{\, n}}}}^{{}}$ f_i g_j

(18)

The polynomial h is also denoted by f *_n g or simply by f * g if not ambiguous.

Remark 2 Observe that the product of f by g is

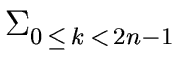p = $\displaystyle \Sigma_{{{0 \, \leq \, k \, < \, 2n-1}}}^{{}}$ p_k x^k

(19)

where for every k = 0^...2n - 2 the coefficient p_k is given by

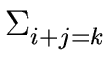p_k = $\displaystyle \Sigma_{{{i+j = k}}}^{{}}$ f_i g_j

(20)

We can rearrange the polynomial p as follows.

p	=	$\displaystyle \Sigma_{{{0 \, \leq \, k \, < \, n}}}^{{}}$ (p_k x^k) + xⁿ $\displaystyle \Sigma_{{{0 \, \leq \, k \, < \, n-1}}}^{{}}$ (p_k+n x^k)
	=	$\displaystyle \Sigma_{{{0 \, \leq \, k \, < \, n}}}^{{}}$ (p_k + p_k+n xⁿ) x^k

(21)

Therefore we have

f * g $\displaystyle \equiv$ fg mod xⁿ-1

(22)

Example 5 Let R = $\mbox{${\mathbb Z}$}$ /5 $\mbox{${\mathbb Z}$}$ , n = 4, u $\in$ R and consider the polynomials

f = x³ + 1 and g = 2x³ + 3x² + x + 1.

(23)

Assume that we want to multiply f and g modulo x⁴ = u. Then we have to arrange the product fg in a form q(x⁴ - u) + r where r has degree less than 4. We obtain

f g	=	2 x $\displaystyle \sp$ 6 + 3 x $\displaystyle \sp$ 5 + x $\displaystyle \sp$ 4 + 3 x $\displaystyle \sp$ 3 + 3 x $\displaystyle \sp$ 2 + x + 1
	=	(2x² + 3x + 1)(x⁴ - u) + 3x³ + 3x² + x + 1 + (2x² + 3x + 1)u
	=	(2x² + 3x + 1)(x⁴ - u) + 3x³ + (3 + 2u)x² + (1 + 3u)x + (1 + u)

(24)

For u = 1 we obtain

f * g = 3x³ + 4x + 2

(25)

Lemma 2 For f, g $\in$ R[x] univariate polynomials of degree less than n we have

DFT(f*g) = DFT(f )DFT(g)

(26)

where the product of the vectors DFT(f ) and DFT(g) is computed componentwise.

Proof. Since f * g and f g are equivalent modulo xⁿ - 1, there exists a polynomial q $\in$ R[x] such that

f * g = f g + q (xⁿ - 1)

(27)

Hence for i = 0^...n - 1 we have

(f * g)( $\displaystyle \omega^{{i}}_{{}}$ )	=	f ( $\displaystyle \omega^{{i}}_{{}}$ ) g( $\displaystyle \omega^{{i}}_{{}}$ ) + q( $\displaystyle \omega^{{i}}_{{}}$ )(( $\displaystyle \omega^{{{i \, n}}}_{{}}$ - 1)
	=	f ( $\displaystyle \omega^{{i}}_{{}}$ ) g( $\displaystyle \omega^{{i}}_{{}}$ )

(28)

by application of Lemma 1. $\qedsymbol$

Remark 3 Consider the multi-point evaluation map

E : $\displaystyle \left\{\vphantom{ \begin{array}{rcl} R[x] & \longmapsto & R^n \\ ... ...1), f({\omega}), f({\omega}^2), \ldots, f({\omega}^{n-1})) \end{array} }\right.$ $\displaystyle \begin{array}{rcl} R[x] & \longmapsto & R^n \\ f & \longmapsto & (f(1), f({\omega}), f({\omega}^2), \ldots, f({\omega}^{n-1})) \end{array}$

(29)

Its kernel is generated by xⁿ - 1. Since E is surjective, it follows that

R[x]/ $\displaystyle \langle$ xⁿ - 1 $\displaystyle \rangle$ $\displaystyle \simeq$ Rⁿ

(30)

(which is not a surprise!) and DFT realizes this isomorphism.

If R is a field, then this a special case of the Chinese Remaindering Theorem where m_i = x - $\omega^{{i}}_{{}}$ for i = 0^...n - 1.