

Next: A modular Gcd Algorithm in
Up: Advanced Computer Algebra: The resultant
Previous: Modular Gcd Algorithms in [x]
Algorithm 3
can be adapted to the case of more than one variable provided
that we have a gcd algorithm in polynomial rings of the
form
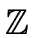 /
/ p
p [x1,..., xn].
Algorithm 4
computes the gcd of two polynomials
f, g
[x1,..., xn].
Algorithm 4
computes the gcd of two polynomials
f, g 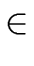
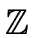 [x1,..., xn]
with this assumption.
Observe that Algorithm 4
takes as input any couple of multivariate polynomials over
[x1,..., xn]
with this assumption.
Observe that Algorithm 4
takes as input any couple of multivariate polynomials over
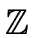 ,
primitive or not.
,
primitive or not.
Algorithm 4
relies also on the following technical assumptions.
-
f
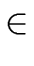
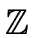 [x1,..., xn]
[x1,..., xn]  content
content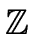 (f )
computes the content of a multivariate polynomial over
(f )
computes the content of a multivariate polynomial over
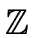 ,
that is the gcd of its coefficients.
We make the same conventions as for the univariate case.
See Definition 3.
,
that is the gcd of its coefficients.
We make the same conventions as for the univariate case.
See Definition 3.
-
(f
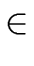
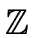 [x1,..., xn], c
[x1,..., xn], c 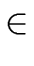 R)
R)  f exquo c is
the exact division of a polynomial by an integer. That is, assuming
that c divides f, the value returned by
f
f exquo c is
the exact division of a polynomial by an integer. That is, assuming
that c divides f, the value returned by
f 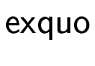 c is the polynomial
g such that
f = c g.
c is the polynomial
g such that
f = c g.
- We need to specify what the leading coefficient and the degree of a multivariate
polynomial are. To do so, we view polynomials as linear combinations of monomials
with coefficients in
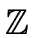 . To decide which is the leading monomial
(and thus which is the leading coefficient) we assume that the
variables are totally ordered, say
x1 > ... > xn.
Then to order monomials we use the lexicographic ordering induced by
x1 > ... > xn.
. To decide which is the leading monomial
(and thus which is the leading coefficient) we assume that the
variables are totally ordered, say
x1 > ... > xn.
Then to order monomials we use the lexicographic ordering induced by
x1 > ... > xn.
-
f
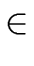
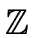 [x1,..., xn]
[x1,..., xn]  lclex(f )
returns the leading coefficient of f w.r.t. the lexicographic ordering
induced by
x1 > ... > xn.
lclex(f )
returns the leading coefficient of f w.r.t. the lexicographic ordering
induced by
x1 > ... > xn.
-
f
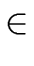
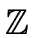 [x1,..., xn]
[x1,..., xn]  deglex(f )
returns the degreeof f w.r.t. the lexicographic ordering
induced by
x1 > ... > xn. That is the exponent vector
of the leading monomial of f.
deglex(f )
returns the degreeof f w.r.t. the lexicographic ordering
induced by
x1 > ... > xn. That is the exponent vector
of the leading monomial of f.
Algorithm 4
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] $f,g \in ...
...n} $h$\ \\
\> \> $(m, g_m)$\ := $(m \, p, w)$\ \\
\end{tabbing}\end{minipage}}](img138.png)
Observations.
- The assumption of primtive input polynomials has been relaxed.
However by dividing f and g by their contents, we turn back
to the primitive case.
- The combine(p, m)(gp, gm) is in fact a series
of CRA: one per monomial. Remember the case of the
fast multication in
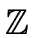 [x] based on the FFT.
[x] based on the FFT.
- Note that the result computed by the Chinese remainder algorithm (CRA) must be expressed
in the symmetric range of the integers modulo m p so that negative integer
coefficients in w can be reconstructed as well as positive ones.
- The termination test can be improved in the sense that it may not be worth
trying it before a certain amount of modular gcd have been computed.
In practice, one could wait for the following stabilization condition
which will necessarily happen.
See [KM99] for more details and proofs.


Next: A modular Gcd Algorithm in
Up: Advanced Computer Algebra: The resultant
Previous: Modular Gcd Algorithms in [x]
Marc Moreno Maza
2004-04-27
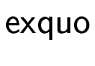 c is the polynomial
g such that
f = c g.
c is the polynomial
g such that
f = c g.