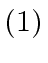
- Show that the above algorithm
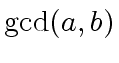 computes the GCD of
computes the GCD of 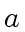 and
and 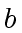 .
.
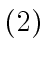
- Assume that
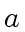 and
and 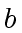 are two machine integers.
Let
are two machine integers.
Let 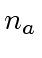 and
and 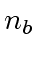 the number of bits (in binary-expansion) of
the number of bits (in binary-expansion) of 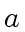 and
and 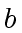 respectively.
Give an upper bound for the number of machine word operations
(comparison of two machine integers, subtraction, shift,
accessing a bit of a machine integer) needed for
computing
respectively.
Give an upper bound for the number of machine word operations
(comparison of two machine integers, subtraction, shift,
accessing a bit of a machine integer) needed for
computing
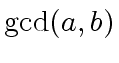 .
.
- Adapt the above algorithm for computing GDCs in
![$ {\mbox{${\mathbb{Z}}$}}/2{\mbox{${\mathbb{Z}}$}}[x]$](img21.png) , that is
for univariate polynomials with integer coefficients modulo
, that is
for univariate polynomials with integer coefficients modulo 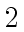 .
.
Marc Moreno Maza
2008-03-18
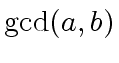 computes the GCD of
computes the GCD of 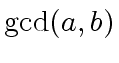 .
.
![$ {\mbox{${\mathbb{Z}}$}}/2{\mbox{${\mathbb{Z}}$}}[x]$](img21.png) , that is
for univariate polynomials with integer coefficients modulo
, that is
for univariate polynomials with integer coefficients modulo