Next: Exercise 2 Up: Exercise 1 Previous: Questions
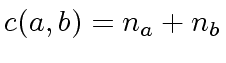 .
Observe that after in each recursive call,
this quantity deceases strictly.
So, it is enough to prove the algorithm
by induction on
.
Observe that after in each recursive call,
this quantity deceases strictly.
So, it is enough to prove the algorithm
by induction on 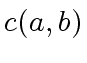 , which is easy.
, which is easy.
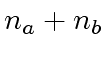 recursive calls.
recursive calls.
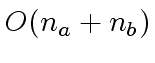 operations in
operations in
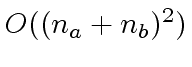 word operations.
word operations.
![$ {\mbox{${\mathbb{Z}}$}}/2{\mbox{${\mathbb{Z}}$}}[x]$](img21.png) :
:
==
1 ifthen return
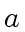
2 ifand
then return
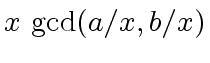
3 ifand
then return
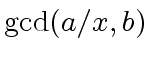
3 ifand
then return
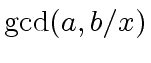
4 ifthen return
else return
Marc Moreno Maza